第３１６問の解答

問題　［ 平面図形］

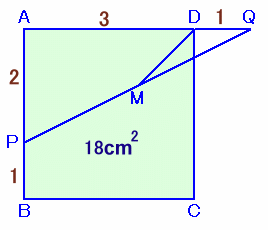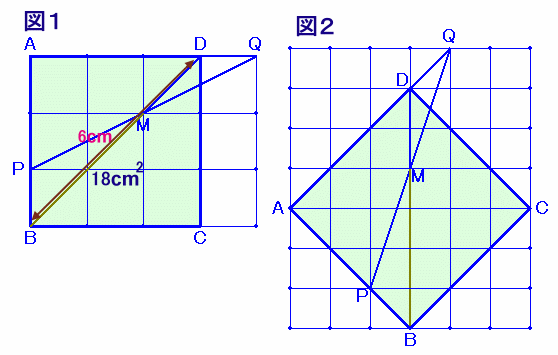
問題図 左図のような正方形ＡＢＣＤがあります。

いま、辺ＡＢ上にＡＰ：ＰＢ＝２：１となる点Ｐをとり、さらに辺ＡＤの延長線上（Ｄの右側）にＰＢ＝ＱＤとなるような点Ｑをとります。また、ＰＱ上に中点Ｍをとります。

正方形ＡＢＣＤの面積が１８cm2であるとき、図のＤＭの長さを求めて下さい。

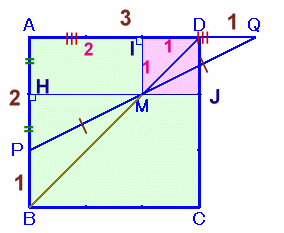
解答例１

トトロ＠Ｎさん、あんみつさん、もくさくさん、まるケンさん、ねこやんさん、 ふじさきたつみさん、さねかづらさん、他

下図のように格子を描きます。

参考図１

すると、Mは正方形ABCDの対角線DBを１：２に内分する点であることが分かります。
（厳密には、解答例２のように証明する必要がありますが。）

ABCDの面積＝１８cm2より、BD2＝ABCDの面積×２＝３６、
よって、BD＝６cm。

従って、DM＝BD×1/3＝２cm　となります。

答：　２cm

以上

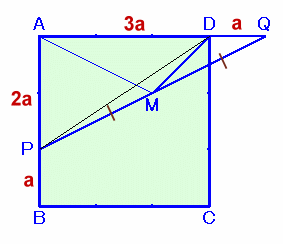
解答例２

Taroさん、小杉原 啓さん、おりくんさん、小西孝一さん、ミミズクはくず耳さん、フランク長いさん、kokoさん、大岡　敏幸さん、ななしのぞうさん、あほあほまんさん、他　多数

点Ｍより、ＡＢ、ＡＤ、ＤＣに下ろした垂線の足を、Ｈ、Ｉ、Ｊとします。
また、ＰＢの長さを１とおきます。

参考図２

△ＱＡＰについて中点連結定理により、
　ＡＩ＝ＩＱ＝２、ＡＨ＝ＨＰ＝１。

従って、ＩＤ＝ＡＤ−ＡＩ＝１、ＩＭ＝ＡＨ＝１。

従って、四角形ＩＭＪＤは１辺の長さがＰＢと等しい正方形となります。

従って、正方形ＩＭＪＤ＝正方形ＡＢＣＤ×1/9＝１８×1/9＝２cm2。

よって、ＤＭ2＝正方形ＩＭＪＤ×２＝４cm2、
　ＤＭ＝２cm　と分かります。

解答例３

うっしーさん、M.Hossieさん、 他

点AとM、および点DとPを結びます。
また、PBの長さをaとおきます。

参考図３

題意より、AP＝PB×２＝２a、AD＝AB＝PB×３＝３ａ、ＤＱ＝ＰＢ＝ａ。

また、正方形ＡＢＣＤの面積＝１８cm2より、（３ａ）2＝１８、
よって、ａ2＝２。

直角三角形APQについて、ピタゴラスの定理より、
　ＰＱ2＝ＡＰ2＋ＡＱ2＝（２ａ）2＋（４ａ）2＝２０ａ2、
よって、ＰＭ2＝ＭＱ2＝ＰＱ2×1/4＝５ａ2。

直角三角形APＤについて、ピタゴラスの定理より、
　ＤＰ2＝ＡＰ2＋ＡＤ2＝（２ａ）2＋（３ａ）2＝１３ａ2。

さて、△ＡＰＱについてパップスの中線定理より、
　（ＤＰ2＋ＤＱ2）×1/2＝ＤＭ2＋ＰＭ2
　（１３ａ2＋ａ2）×1/2＝ＤＭ2＋５ａ2
よって、
　ＤＭ2＝２ａ2＝４　となり、ＤＭ＝２cmと分かります。

（その他の解法）