第３１７問の解答

問題　［ 平面図形］

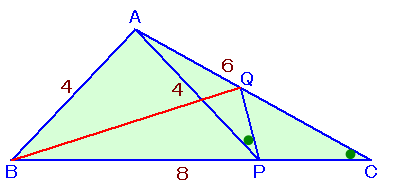問題図 左図のような△ＡＢＣがあります。

いま、辺ＢＣ上に点ＰをＡＢ＝ＡＰとなるように、
また、辺ＡＣ上に点Ｑを∠ＡＰＱ＝∠ＢＣＡとなるようにとりました。

このとき、ＢＱの長さを求めて下さい。

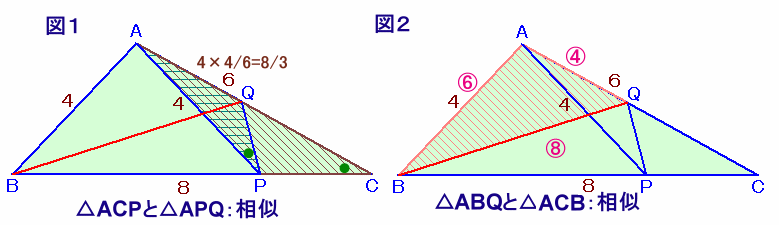
解答例１

トトロ＠Ｎさん、拓パパさん、 他

参考図１

△ACPと△APQについて、∠ACP＝∠APQ、∠CAP＝∠PAQ（共通）より相似。
よって、AQ＝AP×AP/AC=４×４/６＝８/３。

△ABQと△ACBについて、∠BAQ＝∠CAB（共通）、AB：AQ＝４：８/３＝６：４＝AC：ABより相似。

従って、BQ＝AB×BC/AC＝４×８/６＝１６/３cm　となります。

答：　１６/３ｃｍ

以上

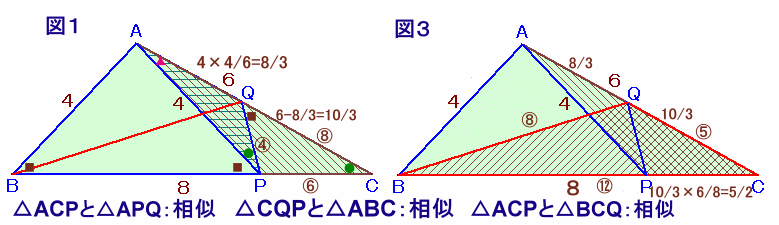
解答例２

永井　暁さん、Miki Sugimotoさん、有無相生さん、あさみかずみさん、うーちゃんさん、あほあほまんさん、大岡　敏幸さん、 他

参考図２

△ACPと△APQが相似、AQ＝８/３、までは解答例１と同じ。
従って、CQ＝AC−AQ＝６−８/３＝１０/３。

∠CQPは△APQの外角だから、∠CQP＝∠PAC＋∠APQ＝∠PAC＋∠BCA、
∠APBは△ACPの外角だから、∠APB＝∠PAC＋∠BCA。
よって、∠CQP＝∠APB＝∠ABC。

△CQPと△ABCについて、∠CQP＝∠ABC、∠QCP＝∠BAC（共通）より相似。
よって、CP＝CQ×AC/BC＝１０/３×６/８＝５/２。

△ACPと△BCQについて、∠ACP＝∠BCQ（共通）、AC：CP＝６：５/２＝８：１０/３＝BC：CQより相似。

よって、BQ＝BC×AP/AC＝８×４/６＝１６/３cm　と分かります。

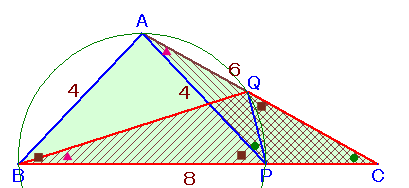
解答例３

sugitakukunさん、ステップ　ばい　ステップさん、 他

参考図３

∠ABP＝∠APB＝∠ACP＋∠PAC＝∠APQ＋∠PAC＝∠PQC、
よって、∠ABP＋∠AQP＝∠PQC＋∠AQP＝１８０度。

従って、四角形ABPQは、ある円に内接することが分かります。

従って、∠PAC＝∠QBC。

△ACPと△BCQについて、∠ACP＝∠BCQ（共通）、∠PAC＝∠QBCより相似。

以下、解答例２と同様。

（その他の解法）