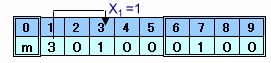
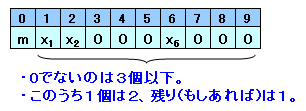
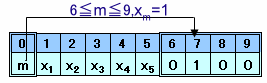第３１８問の解答

問題　［整数の性質］

ある１０ケタの整数Ａがあります。この整数は、次のような性質を持っています。
  • 先頭の数は、Ａで使われた０の個数
  • ２番目の数は、Ａで使われた１の個数
  • ３番目の数は、Ａで使われた２の個数
    　　　　　　・
    　　　　　　・
  • １０番目の数は、Ａで使われた９の個数

では、この整数Ａを求めて下さい。

解答例１

monさん、ミミズクはくず耳さん、ちば けいすけさん、有無相生さん、M.Hossieさん、ねこやんさん、フランク長いさん、スモークマンさん、ハラギャーテイさん、tomhさん、うっしーさん、大岡　敏幸さん、他　多数

整数Ａの各桁の数字をx0、x1、・・・、x9とします。

参考図１

xkが整数Ａで使われたkという数字の個数だから、その和はＡの桁数である１０に等しい。
また、xk>0のとき、kという数字が整数Ａにxk個存在するので、xk個の数字がk個あることになるので、k・xkの和もAの桁数１０と等しい。

以上より、次の２式が成り立ちます。

  • Σk=0..9xk＝１０　・・・　（１）

  • Σk=0..9k・xk＝１０　・・・　（２）

さて、０の個数に着目して考えましょう。

もし０の個数が０ならば、x0＝０となり、０という数字が１個はあることになって矛盾します。
また、０の個数が１０ならば、全ての桁の数字が０となるので、x0＝０となって矛盾。

従って、１≦x0≦９となります。　・・・　（３）

さて、k=1〜9でxk>0となるkの個数をNとします。
もし、N≧4とすると、1≦p<q<r<s≦9でxp、xq、xr、xs>0となる数字p、q、r、sが存在します。
このとき、
　Σk=0..9k・xk≧p・xp＋q・xq＋r・xr＋s・xs≧1・xp＋2・xq＋3・xr＋4・xs＝1+2+3+4＝１０

ところが、（２）が成り立つので、上式より、p=1、q=2、r=3、s=4、xp=xq=xr=xs=1が成り立つことになります。
これは、１という数字が少なくとも４個存在することとなり、x1=1（p=1のときxp=1）と矛盾します。

よって、N≦３が成り立ちます。　・・・　（４）

ところで、Nはxk>0となるkの個数だったので、これより０という数字が、１ ０−（１＋３）＝６個以上存在することになり、６≦x0≦９となります。　・・・　（５）

さて、m＝x0とおきます。（５）より、６≦m≦９が成り立ちます。
すると、mという数字が先頭に存在するので、xｍ>0となります。

もしxｍ≧２とすると、m・xｍ≧６・２>１２となり、（２）に反しますから、xｍ＝１となります。
また、もし６≦k≦９、k≠mでxk>0となるものが存在したら、
　m・xｍ＋k・xk≧６・１＋６・１>10となって、（２）に反します。
従って、６≦k≦９では、k=m以外はxk＝０となります。

参考図１−２

さて、上記からm(6≦m≦9)の桁に１という数字が１個以上存在することになります。
従って、x１>0となりますが、もしx１＝１とすると、さきほどの１個と合わせて数字１が２個は存在することになるので、x１＝１に反します。よって、x１≧２。

参考図１−３

そこで、ｊ＝x１とし、ｊ≧３とすると、１・x１＋j・xj＋m・xm≧１・３＋３・x１＋６・１＝１２となり（２）に反します。
よって、x１＝２と決まります。

従って、２という数字が存在するのですが、この個数は１個でないと上記同様（２）に反することになるので、
　x2＝１と決まります。

参考図１−４

さて（４）から、これ以上０でない数字は存在しないことになります。
よって（２）より、
　０・m＋１・２＋２・１＋m・１＝１０
　４＋m＝１０
従って、m＝６と決まります。

以上から、求める整数A＝６２１０００１０００と決まります。
また、この６２１０００１０００は題意を満たすので、求める解となり、またこれ以外に解はありません。

答：　６２１ ０００１０００

以上

解答例２

高橋　道広さん、 他

本問を次のように一般化して解を求めます。

(問題)

(n+1)個の整数の組があり、

  • 各xk（k=0、・・、n)が 、この整数の組の中にあるkの個数に等しい

となるものを求む。

（解）

  • n≦２のとき：解なし
  • n＝３のとき：２０２０、１２１０の２個
  • n＝４のとき：２１２００
  • n＝５のとき：解なし
  • n≧６のとき：(n-3)２１0・・(n-6個の ０)１０００

　

解答例１と同様に、各桁の数字をx0、x1、・・・、xnとします。

(ａ)　x0≠n、n+1ではない

  • x0＝n+1とすると、x0＝x1＝、・・・、＝xn＝ ０となり 、x0＝0はx0＝n+1と矛盾。

  • x0＝nとすると、x0＝n、x1＝、・・・、＝xn＝ ０となり、nという数字が１個存在することになり、xn＝0と矛盾。

(ｂ) 各xｋ(１≦k≦n)のなかで0でない個数をＸ個とすると 、１≦Ｘ≦３。

まず、x0≠０が成り立つので、x0という数字は１個以上存在します。
従って、１≦Ｘ。

xｋのなかで0でないＸ個の和をSとします。
解答例１の（１）と同様、x0＋x1＋x2＋・・・＋xn＝n+1　 ・・・　（１）

また、n個ある各xｋのなかで０でない個数がＸということは、
　０の個数であるx0＝n-Xとなります。　・・・　（２）

（１）より、
　x0＋Ｓ＝n+1、
　n-X＋Ｓ＝n+1、
よって、Ｓ＝Ｘ＋１　となります。　　・・・　（３）

（３）より、x1、x2、・・・、xnのうち０でないＸ個の整数の和がＸ＋１ということになり、
これらの整数は、「２が１個、残りは（もしあれば）全て１」ということになります。　　・・・　（４）

従って、０でない数字があるとすれば、最も多くて、１、２、n-Xの３個となるので、
　Ｘ≦３となります。

(ｃ) Ｘ＝１、２、３の各場合に分けて組を求める。

参考図２

  • Ｘ＝1のとき

xｋ(k≧１)で０でないのが１個のみで、その数字は２ということになります。

ということは、２の数字が存在するので、x2>０、従って、x2＝２に他なりません。
よって、x0＝２となり、（２）より、x0＝２＝n-1、従ってn＝３となります。

従って、このケースの解は、２０２０となります。
　

  • Ｘ＝２のとき

xｋ(k≧１)で０でないのが２個で、その数字は１と２。
またこの和はＸ＋１＝３だから、考えられるケースは、x1＝２、x2＝１またはx1＝１、x2＝２の２通り。

  1. x1＝２、x2＝１のとき

２個ある数字１のひとつはx0＝１で 、（２）より、x0＝１＝n-２、よってn＝３となります。
従って、このケースの解は、１２１０となります。

  1. x1＝１、x2＝２のとき

２個ある数字２のひとつはx0＝２で 、（２）より、x0＝２＝n-２、よってn＝４となります。
従って、このケースの解は、２１２００となります。

  • Ｘ＝３のとき

xｋ(k≧１)で０でないのが３個で、その数字は１と２およびx0＝n-３。
このとき、n-３>２となるので、n≧５。

（４）より、x1、x2、xn-3のうち２が１個、残り２ 個は１となります。
従って、数字１が２個以上あるので、x1＝２、x2＝xn-3＝１に 他なりません。

従って、このケースの解は、(n-3)２１0・・(n-6個の ０)１０００となります。

とくに、n＝９のとき、本問の場合となり、解は６２１０００１ ０００となります。

解答例３

長野　美光さん、まるケンさん、中村明海さん、ｋｕｒｉ、 他

１０桁の整数N=N0N1・・・N9に対して、X＝X0X1・・・X9(Xk：Nkの中でkに等しい数字の個数）を対応させます。
ただし、N0=N1=・・・=N9＝nのときは、Xn=10、Xk=0（k≠n）となりますが、このときは同様な計算を続けて、X＝９ ００００００００１を対応させます。
（なお、この１０桁の整数には、０００００５６７８９など先頭に０が続く場合を含むことにします。）

参考図３

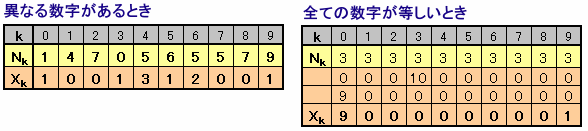
すると、Xの各桁Xkは０≦Xk≦９となりますので、やはり１ ０桁の整数となります。

このとき、ある１０桁の整数a1から出発して対応する１０桁の整数を次々とつなげていきます。
１０桁の整数は有限個ですから、この連鎖はどこかで同じ整数が現れる筈ですので、途中から繰り返しが発生することになります。

この連鎖をグループ１と定義します。
また、途中からグループ１に含まれる整数に合流する整数もグループ１に含めることにします。

１０桁の整数全てを、このようなグループに分類していくと、必ず有限個のグループに分けられることになります。

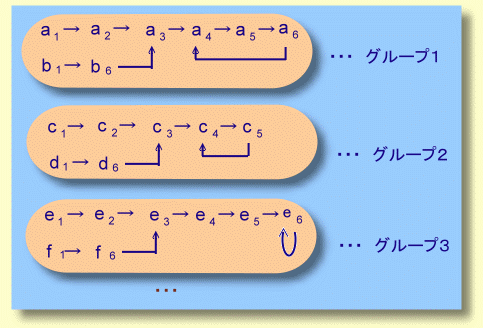
参考図３−２

さて、本問では、これらのグループの中に上図グループ３の場合のように、繰り返し周期が１（対応する整数が元の整数と等しい）となるものが存在するので、これを求めなさいということになります。

そこで、適当な整数を出発点に連鎖を計算していけば、どこかで求める整数が見つかる筈です。
では、ＥＸＣＥＬを用いて計算してみます。

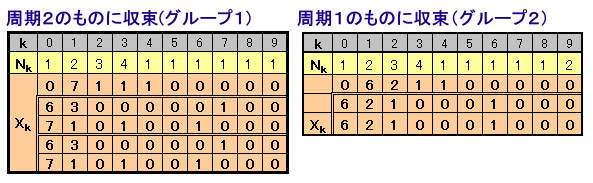
参考図３−３

すると、上図のように、

  • ６３０００００１００⇔７１０１００１０００という周期２のものに収束する　・・・　グループ１

  • ６２１０００１０００という周期１のものに収束する　・・・　グループ２

の２グループに分類できそうです。

従って、グループ２の６２１０００１０００が解ということになりそうです。

そこで、本当に上記２グループしかないことを証明してみましょう。

任意の１０桁の整数に対応する整数は、
　各桁の数字Ｘkは、０≦Ｘk≦９でかつΣk=0..9Ｘk＝１ ０　・・・・　（１）
となります。
元の整数もこの整数と同じグループに属するのですから、はじめから（１）の条件が成立する１０桁の整数だけを考えても差し支えありません。

さて、もし０でない数字が５個以上あったとすると、（１）より、０でない数字の合計が１０になるわけですが、それらの和≧１＋２＋３＋４＋５＝１５なので矛盾。

従って、０でない数字は４種類以下になります。

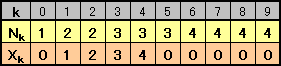
参考図３−４

すると、この次に対応する整数は０が６個以上となりますので、最初から０が６個以上の場合に絞っても差し支えないことになります。

そこで、１０桁の整数で各桁の合計が１０となるもので、かつ０が６個以上の場合について場合分けして調べることにしましょう。
数字を大きい順に並べても次に対応する整数は変わりませんで、便宜上、数字の大きい順に表し、また０を省略することにします。

場合分けをすると、次の１１種類になります。また、対応する整数も求めてみます。

  1. ９１　　　→　８１１　　→　７２１　　→　７１１１　→　６３１

  2. ８２　　　→　８１１　　→　７２１　　→　７１１１　→　６３１

  3. ８１１　　→　７２１　　→　７１１１　→　６３１

  4. ７３　　　→　８１１　　→　７２１　　→　７１１１　→　６３１

  5. ７２１　　→　７１１１　→　６３１

  6. ７１１１　→　６３１　　→　７２１　　→　７１１１　→　６３１

  7. ６４　　　→　８１１　　→　７２１　　→　７１１１　→　６３１

  8. ６３１　　→　７１１１　→　６３１

  9. ６２２　　→　７２１　　→　７１１１　→　６３１

  10. ６２１１　→　６２１１

  11. ６１１１１→　５４１　→　６３１　　　→　７１１１　→　６３１

以上から、最初に推測した２グループしかないことが分かります。