第３１９問の解答

問題　［場合の数］

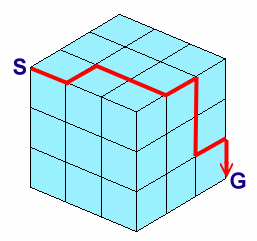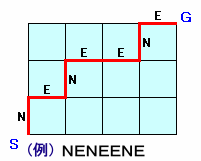
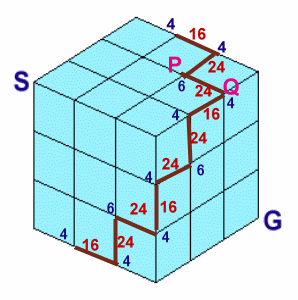
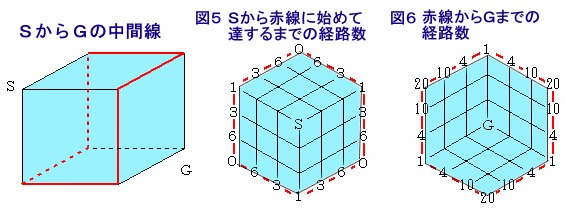
問題図 左図のような一辺の長さが３cmの立方体があり、各面が一辺１cmの正方形のマス目で区切られています。

このとき、図中のＳの位置からＧの位置まで、立方体の辺上および各面のマス目上を通って最短距離（９cmですね）で進む方法（図中にはその一例が赤線で示されています）は何通りあるでしょうか。

解答例１

おかひで博士さん、ＩＣさん、tropicanaさん、takuさん、　あんみつさん、 他

まず、平面の場合で考えます。

参考図１

　

上図のように縦m×横nのマス目からなる格子線上で対角線を結ぶ最短距離は、
　上へ進む場合をN、右へ進む場合をE
で表すと、m個のNとn個のEを並べる方法の数に帰着されます。

従って、この場合は、（m+n）!/m!n!で求まります。

本問の場合、立方体の中は通れませんので上記式をそのまま拡張することはできません。

参考図１−２

そこで、上記図１のように各面に名前をつけます。

そして、図２のように展開図で考えると、ＳからＧへ至る最短経路は、
２面分（縦３×横６）の最短経路と考えられます。

２面の組み合わせは、　ca、cd、ba、be、fd、fe　の６通りあります。

それぞれの最短経路数＝（３＋６）!/３!６!＝８４通りなので、
　合計８４×６＝５０４通りとなります。

ただし、上記の数え方には、辺を共通にする組み合わせが６通り存在します。
（caとcd、baとbe、beとfe、fdとfe、baとca、cdとfd）

この場合の経路数は、それぞれ１面＋１辺なので、(３＋３)!/３!３!×６＝２０×６＝１２０通り。

従って、求める経路数は、５０４−１２０＝３８４通りとなります。

答：　３８４通り

以上

解答例２

Miki Sugimotoさん、ヌオの母さん、ミミズクはくず耳さん、小西孝一さん、ほげさん、まるケンさん、M.Hossieさん、ただの酔っぱらいさん、ふじさきたつみさん、Taroさん、トトロ＠Ｎさん、 他

格子状の各点を通る経路数について、次々と加算していって求めます。

参考図２

図３は、１面の場合です。

図４で各面について計算していくと、Ｇの手前の点では、１２８通りとなります。

Ｇへは、３方向から合流するので、合計１２８×３＝３８４通りと求まります。
　

解答例３

有無相生さん、ねこやんさん、 他

辺を完全に通る個数によって場合分けします。

参考図３

  • ３辺を通る場合：

Ｇを通る辺は３本、それぞれにつき面の２辺を通る方法は２通り。
よって、３×２＝６通り。
（または、３方向に進む順番を決める方法＝３!＝６通り）

  • １辺のみを通る場合

辺の数＝Ｓを通るものが３本＋Ｇを通るものが３本＝計６本
それぞれ、３×３のマス目の最短経路２０通り−２辺を通る２通り＝１８通り。

従って、合計＝１８×６＝１０８通り。

  • １辺も通らない場合

通る面の組み合わせは６通り。
２面を通り、辺を完全に通らないようにするには、上図のように２ケースに分けて考えると、
　９×３＋３×６＝４５通り。

従って、合計＝４５×６＝２７０通り。

従って、求める経路数＝６＋１０８＋２７０＝３８４通りとなります。

解答例４

中村明海さん、 他

ＳＧの中間地点を含む区間で区切って考えます。

参考図４

上図では、Ｓから４区間で到達する点と、Ｇから４区間で到達する点を結ぶ線上を通る場合の数を、
それぞれ計算しています。

例えば、
　ＳからＰへは２×２の最短経路＝（２＋２）!/２!２!＝６通り、
　ＱからＧへは１×３の最短経路＝（１＋３）!/１!３!＝４通り、
従って、ＰＱを通るのは、６×４＝２４通りという具合です。

隠れている面についても対象性を考慮して求めると、
　合計１６×６＋（２４＋２４）×６＝３８４通りになります。

解答例５

長野　美光さん、 他

Ｓから赤線（中間線）まで と、赤線からＧまでを考えます。

参考図５

図５では、Ｓから赤線の各点に始めて達するまでの経路数、
図６では、赤線の各点からからＧまでの経路数を求めています。

従って、求める経路数の合計は、これらの掛け算を加えて、
　（4×6＋10×3＋20×1＋10×3＋4×6）×３＝３８４通りとなります。