第３２０問の解答

問題　［場合の数］

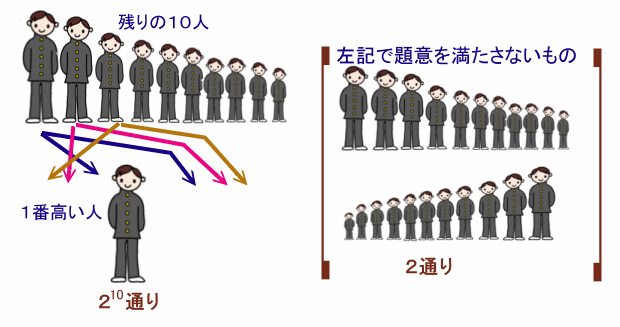
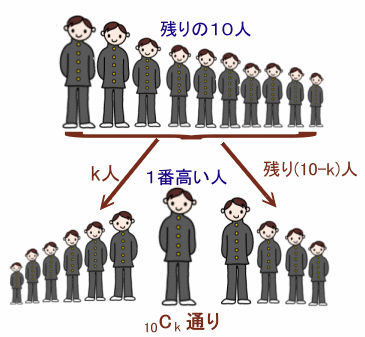
問題図 背の高さが違う１１人の生徒がいます。

この１１人の生徒が１列に並ぶとき、左図のように「山型」になるような並び方は何通りあるでしょうか？

解答例１

小杉原 啓さん、ミミズクはくず耳さん、拓パパさん、あんみつさん、Taroさん、ponta55555さん、ねこやんさん、中村明海さん、小西孝一さん、高橋　道広さん、M.Hossieさん、とりやまさん、ωさん、 他

１１人を大きい順に並べて、まず１番背の高い人を選びます。

参考図１

  • ２番目に高い人は、１番高い生徒の左右のどちらかに並ぶので２通り、

  • ３番目の生徒は、前の２人の左右いずれかの２通り、
    　　　・・・

  • １０番目の生徒は、それまでの人の左右いずれか２通り。

よって、合計では、２×２×・・・×２＝２10＝１０２４通り。

ただし、このうち、大きい順または小さい順に並ぶ場合の２通りは、山型にはならないので除く必要があります。

従って、求める並び方は、１０２４−２＝１０２２通りとなります。
　

答：　１０２２通り

以上

解答例２

おかひで博士さん、トトロ＠Ｎさん、永井　暁さん、ステップ　ばい　ステップさん、萬田銀次郎さん、ゆんななこさん、あまれっとさん、有無相生さん、ふじさきたつみさん、高校１年さん、 他

１番高い生徒の左右に何人ずつ並ぶかによって場合分けします。

参考図２

１番高い生徒の向かって左側にk人（1≦k≦9）並ぶ場合を考えます。

選び方は、１０人の中からk人選ぶ10Ck通りあります。
残りの(10-k)人は自動的に決まります。
また、これらの生徒の並び方も自動的に決まるので、この場合の並び方は、結局10Ck通りとなります。

従って、合計では、
　10C1＋10C2＋・・・＋10C9
＝（10C0＋10C1＋10C2＋・・・＋10C9＋10C10）-（10C0＋10C10）
＝２10−（１＋１）　・・・　２項定理による
＝１０２４−２
＝１０２２通り
となります。

解答例３

CRYING DOLPHINさん、ちば けいすけさん、ハラギャーテイさん、 他

漸化式で考えます。

n人の場合の並べ方の数を an とすると、 a3 = ２通り。

(k + 1)人の並べ方 ak+1 は、 次の２つの場合があります。

  • k 人並んだ状態ak通りのそれぞれに、それより小さい人を左右どちらかに追加する
    　・・・　２ak+1 通り

  • k 人が大きい順か小さい順に並んでいるときに、それより小さい人を大きい人の隣に 追加する
    　・・・　２通り

従って、ak＋1＝２ak＋２　・・・　（１）

（１）より、　ak＋1＋２＝２（ak＋２）となるので、an＋２は等比数列と分かります。
よって、an＋２＝２n-3（a3＋２）＝２n-3・４＝２n-1。

従って、an＝２n-1−２　通りとなります。

とくに本問では、n＝１１なので、a11＝２10−２＝１０２２通りとなります。