第３２２問の解答

問題　［場合の数］

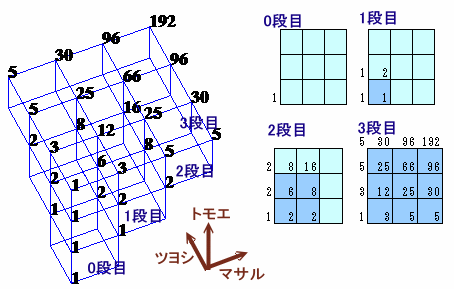
全校生徒９人のある学校で、生徒会長を選挙で選ぶことになりました。

立候補したのはマサルさん、トモエさん、ツヨシ君の３人でしたが、激戦の結果、３人とも３票ずつの得
票となってしまいました。また開票作業中、トモエさんは常に得票数がトップであったそうです。

では、このようになる開票順は何通りあるでしょうか。

解答例１

Taroさん、CRYING DOLPHINさん、Miki Sugimotoさん、トトロ＠Ｎさん、ミミズクはくず耳さん、中村明海さん、長野美光さん、高橋　道広さん、ωさん、小西孝一さん、ねこやんさん、他

３×３×３の立体格子上を通る最短経路で考えます。

参考図１

マサルさん、ツヨシ君、トモエさんの得票をそれぞれx、y、z軸方向に１マス進むことに対応させます。

0段目の隅を1通りとして、1段目→２段目→３段目と順次計算していくと、上図のようになります。
なお、格段の様子を右の図に再掲しました。

よって、求める場合の数は、１９２通りとなります。

　

答：　１９２通り

以上

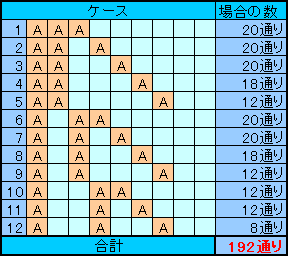
解答例２

あんみつさん、中川　幸一さん、ＩＣさん、モルモット大臣さん、maruhagedonさん、辻。さん、Banyanyanさん、敬＠Ｎさん、M.Hossieさん、ふじさきたつみさん、ステップ　ばい　ステップさん、有無相生さん、フランク長いさん、サンちゃんさん、他

マサルさん、ツヨシ君、トモエさんの得票をそれぞれA、B、Cとして、Aの並び方による場合分けで考え ると、
下記の１２ケースに分かれます。

参考図２

  • ケース１、２、３、６、７の場合　・・・　（ア）
    残りの６個のマスには、BおよびCを自由に配置できる。
    Bを配置すれば、Cは自動的に決まるので、6C3＝２０通り。
    　

  • ケース４、８の場合　・・・　（イ）
    （ア）同様の6C3＝２０通りから、３番目のAより先にBが３個またはCが３個並ぶ２ケースを除く、
    ２０−２＝１８通り。
    　

  • ケース５、９の場合　・・・　（ウ）
    残り６個のマスのうち、最初の４個にはBまたはCが３個並ぶことはできないので、それぞれ２個、
    最後の２マスには、BおよびCが１個づつ、
    よって、4C2×2C1＝６×２＝１２通り。
    　

  • ケース１０、１１の場合　・・・　（エ）
    残り６個のマスのうち、最初の２個にはBまたはCが２個並ぶことはできないので、それぞれ１個、
    最後の２マスには、BおよびCが２個づつ、
    よって、2C1×4C2＝２×６＝１２通り。
    　

  • ケース１２の場合　・・・　（オ）
    残り６個のマスのうち、最初の２個にはBまたはCが２個並ぶことはできないので、それぞれ１個、
    次の２マスにも、同様にBおよびCが１個づつ、最後の２マスにも、同様にBおよびCが１個づつ、
    よって、2C1×2C1×2C1＝２×２×２＝８通り。

従って、合計＝２０×５＋１８×２＋１２×４＋８＝１９２通りとなります。

（その他の解法）