第３２３問の解答

問題　［空間図形］

問題図 左図のような、体積が１００cm3の三角錐Ａ−ＢＣＤがあります。

ある平面でこの三角錐を切断したところ、
　ＡＰ：ＰＢ＝１：１、ＡＱ：ＱＣ＝３：１、ＣＲ：ＲＤ＝２：３
となりました。

頂点Ａを含むほうの立体の体積を求めてください。

解答例１

トトロ＠Ｎさん、かなくんさん、ヒデー王子さん、啓＠Nさん、フランク長いさん、ねこやんさん、他

４点P、Q、R、Sは同一平面上にあるので、この平面と直線BCの交点をTとすると、
PQ、SRもTを通ります。

参考図１

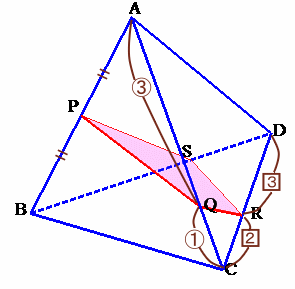
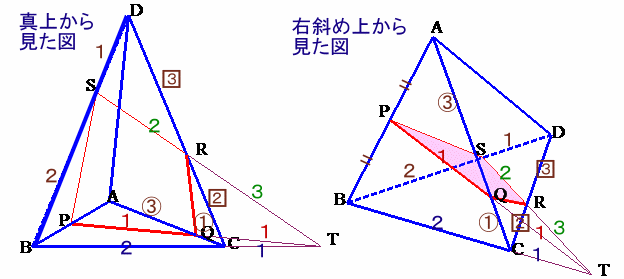
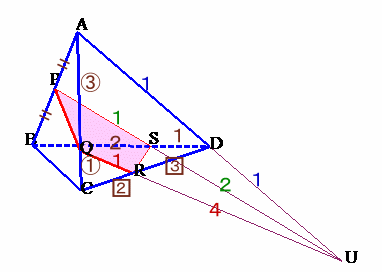
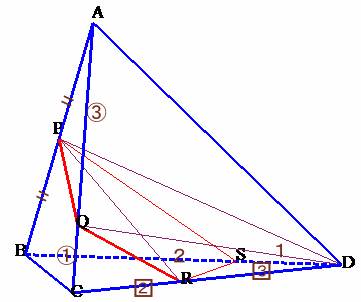
△ABCと直線PTに関してメネラウスの定理より、
　AP/PB×BT/TC×CQ/QA＝１
　１/２×BT/TC×１/３＝１
　BT：TC＝２：３
よって、BC：CT＝２：１。　

△BCDと直線STに関してメネラウスの定理より、
　BT/TC×CR/RD×DS/SB＝１
　３/１×２/３×DS/SB＝１
よって、DS：SB＝１：２。

△BTSと直線CDに関してメネラウスの定理より、
　BC/CT×TR/RS×SD/DB＝１
　２/１×TR/RS×１/３＝１
よって、TR：RS＝３：２。

△PBTと直線ACに関してメネラウスの定理より、
　PA/AB×BC/CT×TQ/QP＝１
　１/２×２/１×TQ/QP＝１
よって、TQ：QP＝１：１。

ここで、△BCDの面積をS、三角錐A−BCDの体積をV（１００cm3）とおきます。

△DSR＝S×１/３×３/５＝S×１/５、
よって、四角形SBCR＝S×４/５。　・・・　（１）

△TRC＝△TSB×１/３×３/５＝△TSB×１/５、
よって、四角形SBCR＝△TSB×４/５。　・・・　（２）

（１）、（２）より、△TSB＝S。

三角錐A−BCDと三角錐P−BTSは、底面の面積が同じで、高さが１/２、
よって、三角錐P−BTS＝V×１/２。

　三角錐T-QCR
＝三角錐P−BTS×１/３×１/２×３/５
＝（V×１/２）×１/１０
＝V×１/２０

従って、
　三角錐A−BCDの下半分
＝三角錐P−BTS−三角錐T-QCR
＝V×１/２−V×１/２０
＝V×９/２０。

従って、
　三角錐A−BCDの上半分
＝V−V×９/２０
＝V×１１/２０
＝１００×１１/２０
＝５５cm3。

答：　５５cm3

以上

解答例２

CRYING DOLPHINさん、ミミズクはくず耳さん、数楽者さん、ふじさきたつみさん、他

４点P、Q、R、Sは同一平面上にあるので、この平面と直線ADの交点をUとすると、
PS、QRもUを通ります。

参考図２

解答例１と同様にして、DS：SB＝１：２。

△ABDと直線PUに関してメネラウスの定理より、
　AP/PB×BS/SD×DU/UA＝１
　１/１×２/１×DU/UA＝１
　DU/UA＝１：２
よって、DU：AD＝１：１。

△APUと直線BPに関してメネラウスの定理より、
　AB/BP×PS/SU×UD/DA＝１
　２/１×PS/SU×１/１＝１
よって、　PS：SU＝１：２。

△AQUと直線CDに関してメネラウスの定理より、
　AC/CQ×QR/RU×UD/DA＝１
　４/１×QR/RU×１/１＝１
よって、QR：RU＝１：４。　

△APQ＝△ABC×１/２×３/４＝△ABC×３/８。

三角錐U-APQと三角錐D-ABCは、底面の面積が３/８で高さが２倍、
よって、三角錐U-APQ＝三角錐D-ABC×３/８×２＝V×３/４。

　三角錐U-DSR＝三角錐U-APQ×１/２×２/３×４/５＝三角錐U-APQ×４/１５。

　求める立体の体積
＝三角錐U-APQ−三角錐U-DSR
＝三角錐U-APQ×１１/１５
＝（V×３/４）×１１/１５
＝V×１１/２０
＝１００×１１/２０
＝５５cm3。

解答例３

ICさん、ちばけいすけさん、みゃんこさん、他

参考図３

問題の立体を３つの立体（三角錐A-PDQ、三角錐P-QRD、三角錐P-SRD）に分割します。
　

△APD＝△ABC×１/２×３/４＝△ABC×３/８。
よって、三角錐A-PDQ＝V×３/８。

△QRD＝△ACD×１/４×３/５＝△ABC×３/２０。
よって、三角錐P-QRD＝V×３/２０×１/２＝V×３/４０。

△SRD＝△BCD×１/３×３/５＝△ABC×１/５。
よって、三角錐P-SRD＝V×１/５×１/２＝V×１/１０。

　求める立体の体積
＝三角錐A-PDQ＋三角錐P-QRD＋三角錐P-SRD
＝V×３/８＋V×３/４０＋V×１/１０
＝V×（１５＋３＋４）／４０
＝V×２２/４０
＝１００×１１/２０
＝５５cm3。

（その他の解法）