第３２４問の解答

問題　［ 平面図形］

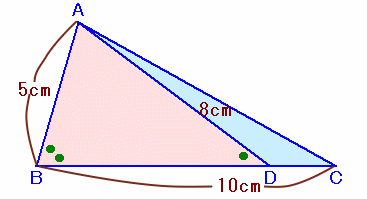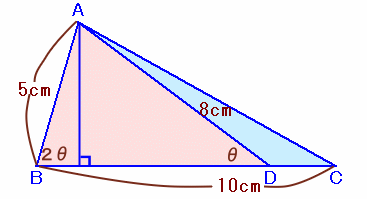
問題図 左図のような、ＡＢ＝５cm、ＢＣ＝１０cmの△ＡＢＣがあります。

いま、∠ＡＤＢの大きさが、∠Ｂの半分の大きさになるように辺ＢＣ上に点Ｄをとったところ、ＡＤ＝８cmとなったそうです。

このとき、△ＡＢＣの面積は何cm2でしょうか。

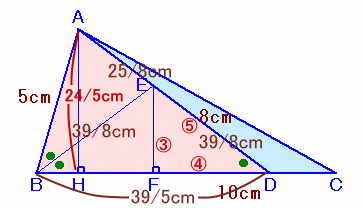
解答例１

Taroさん、ねこやんさん、有無相生さん、フランク長いさん、ななしのごんたさん、萬田銀次郎さん、小西孝一さん、うっしーさん、KOさん、他

∠Bの二等分線とADの交点をEとし、EとAからBCに下ろした垂線の足をFとHとします。

参考図１

∠EBD＝∠EDBより、△EBDは二等辺三角形、よって、EB＝ED。

△AEBと△ABDは、∠Aが共通、∠ABE＝∠ADBより相似。

よって、AE：AB＝AB：AD、
　AE＝AB×AB/AD＝２５/８cm、
従って、EB=ED＝AD-AE＝８−２５/８＝３９/８cm。

また、AB：EB＝AD：BD、
　BD＝AD×EB/AB＝８×（３９/8）/５＝３９/５cm。

よって、ED：FD＝３９/８：３９/１０＝５：４、
従って、△EFDは辺の長さが３：４：５の直角三角形。

△AHDと△EFDは相似より、AH＝AD×３/５＝２４/５cm。

よって、
　△ABC
　＝1/2×BC×AH
　＝1/2×１０×２４/５
　＝２４cm2。

答：　２４cm2

以上

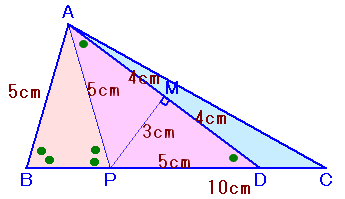
解答例２

CRYING DOLPHINさん、トトロ＠Nさん、ミミズクはくず耳さん、小杉原啓さん、ふじさきたつみさん、omegaさん、他

辺BC上に点Pを、AP＝AB＝５cmとなるようにとります。

参考図２

△ABPは二等辺三角形だから、∠APB＝∠ABP。

∠PAD＝∠APB−∠ADP＝∠ADP、
従って、△PADは二等辺三角形となります。

よって、PD＝AP＝５cm。

ADの中点をMとすると、AM＝DM＝４cm、
よって、△PAMと△PDMは辺の長さが３：４：５の直角三角形となります。

従って、△APD＝1/2×AD×PM＝1/2×８×３＝１２cm2。

△ABCと△APDは、底辺の長さが１０：５＝２：１で、高さは共通、
よって、△ABC＝△APD×２＝１２×２＝２４cm2。

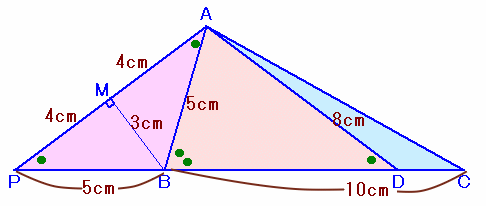
解答例３

ヒデー王子さん、啓＠Nさん、高橋道広さん、他

辺CBを延長して、点PをPB＝AB＝５cmとなるようにとります。

参考図３

△BAPは二等辺三角形となるから、∠BPA＝∠BAP＝∠ABD×1/2＝∠ADB、
よって、△APDも二等辺三角形。

従って、AP＝AD＝８ｃｍ。

ＡＰの中点をＭとすると、ＡＭ＝ＰＭ＝４cm、
よって、△APMと△BPMは、辺の長さが３：４：５の直角三角形、
従って、BM＝３cm。

△APB＝1/2×AP×BM＝1/2×８×３＝１２ｃｍ2。

△ABCと△APBは、底辺の長さが１０：５＝２：１で、高さは共通、
よって、　△ABC＝△APB×２＝１２×２＝２４ｃｍ2。

　

解答例４

Miki Sugimotoさん、ハラギャーティさん、M.Hossieさん、うっしーさん、きょえぴさん、あんみつさん、大岡敏幸さん、他

θ＝∠ADBとおきます。

参考図４

△ABDについて正弦定理より、
　AB/sinθ＝AD/sin2θ
　５/sinθ＝８/２sinθcosθ、
よって、cosθ＝４/５、sinθ＝３/５。

sin2θ＝２sinθcosθ＝２×４/５×３/５＝２４/２５。

従って、
　△ABC
＝1/2×AB×BC×sin2θ
＝1/2×５×１０×２４/２５＝２４ｃｍ2。