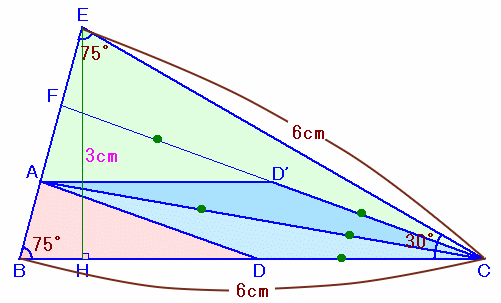
第３２５問の解答

問題　［平面図形］

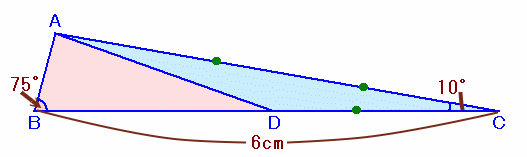問題図 左図のような、∠Ｂ＝７５度、∠Ｃ＝１０度、ＢＣ＝６cmの△ＡＢＣがあります。

いま、辺ＢＣ上に、ＤＣの長さが辺ＡＣの長さの２分の１になるような点Ｄをとりました。

このとき、△ＡＢＣの面積と△ＡＤＣの面積の合計を求めてください。

解答例１

CRYING DOLPHINさん、トトロ@Nさん、佐藤さん、Banyanyanさん、ponta55555さん、ミミズクはくず耳さん、数楽者さん、ふじさきたつみさん、ねこやんさん、M.Hossieさん、航介さん、ステップばいステップさん、他

辺ACを軸にして△ADCを折り返したものを△AD'Cとします。
また頂点Cから３０°に引いた直線とBAの延長線の交点をEとし、
さらにCD'の延長線と線分BEの交点をFとします。

参考図１

△ADCと△AD'Cは合同だから面積は等しい。
よって、△ABC＋△ADC＝△ABC＋△AD'C　・・・　（１）

　∠BEC
＝１８０°−∠ABC−∠ACB
＝１８０°−７５°−３０°
＝７５°
＝∠EBC

よって、△CEBはCE＝BC＝６cmの二等辺三角形。

また、∠ACB＝∠FCA＝１０°より、∠ECF＝３０−２０＝１０°

よって、△ABCと△FECは１辺と挟角が等しいので合同。　・・・　（２）

従って、FC＝ACとなり、△CFAは二等辺三角形となります。

FC＝AC＝CD×２、CD'＝CDよりFD'＝CD×２−CD＝CD、
従って、△FAD'＝△AD'C　・・・　（３）

（１）、（２）、（３）より、
求める面積は二等辺三角形CEBの半分となります。

EからBCに下ろした垂線の足をHとすると、
∠ECH＝３０°だからEH＝EC×１/２＝６cm×１/２＝３cm。

よって、
求める面積＝△CEB×１/２
　＝1/2×BC×AH×１/２
　＝1/2×６×３×１/２
　＝４．５cm2。

答：　４．５cm2

以上

（その他の解法）