第３２７問の解答

問題　［ 平面図形］

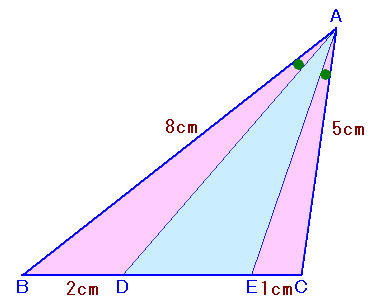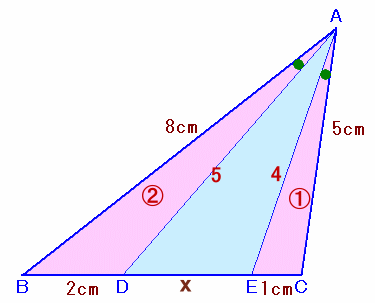
問題図  左図のような、ＡＢ＝８cm、ＡＣ＝５cmの△ＡＢＣがあります。

いま、辺ＢＣ上にＢＤ＝２cm、ＣＥ＝１cmとなる点Ｄ、Ｅをとったところ、∠ＢＡＤ＝∠ＣＡＥとなりました。

では、ＤＥの長さを求めてください。

解答例１

マサルさん、takaisaさん、ねこやんさん、noetherさん、M.Hossieさん、 他

参考図１

△ABDと△AECは、高さが共通で底辺の比はＢＤ：ＥＣ＝２：１、
よって、△ABD：△AEC＝２：１。

∠ＢＡＥ＝∠ＤＡＣより、△ＡＢＥ：△ＡＤＣ＝ＡＢ×ＡＥ：ＡＤ×ＡＣ＝８×４：５×５＝３２：２５。

従って、ＢＥ：ＤＣ＝３２：２５。
ＢＥ−ＤＣ＝２−１＝1cmで、３２−２５＝７より、７が１cmに相当する。

よって、ＢＤ：ＤＥ：ＥＣ＝１４：１８：７。
従って、ＤＥ＝１８/７cmと求まります。

答：　１８/７cm

以上

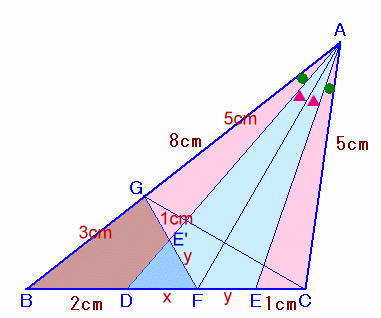
解答例２

ponta55555さん、ＩＣさん、わらいねこさん、 他

∠BACの二等分線と辺BCの交点をFとし、AFを軸に△ACFを折り返したものを△AGFとします。
　

参考図２

角の二等分線の定理より、ＢＦ：ＦＣ＝ＡＢ：ＡＣ＝８：５。

そこで、DF＝ｘ、FE＝ｙとおくと、２＋ｘ：ｙ＋１＝８：５、
よって、５ｘ−８ｙ＝−２　・・・　（１）

ＦＧとＡＤの交点をＥ'とすると、対称性よりＦＥ'＝ＤＥ＝ｙ、Ｅ'Ｇ＝ＥＣ＝１cm。

△GBFと直線ADに関してメネラウスの定理より、
　BD/DF・FE'/E'G・GA/AB＝１
　２/ｘ・ｙ/１・５/８＝１
よって、４ｘ−５ｙ＝０　・・・　（２）

（１）、（２）を解いて、ｘ＝１０/７、ｙ＝８/７を得ます。

よって、DE＝ｘ＋ｙ＝１８/７cmとなります。

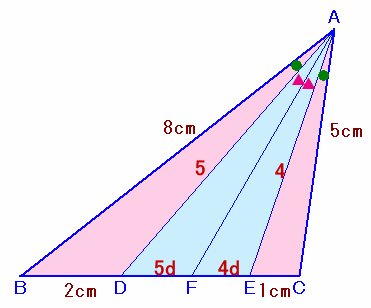
解答例３

有無相生さん、他

∠BACの二等分線と辺BCの交点をFとします。

参考図３

解答例１と同様にして、AD：AE＝５：４。

AFは∠DAEの二等分線でもあるから、DF：FE＝AD：AE＝５：４。
そこで、DF＝５ｄ、FE＝４ｄとします。

AFは∠BACの二等分線だから、BF：FC＝AB：AC＝８：５、
従って、（２＋５ｄ）：（４ｄ＋１）＝８：５。

これをｄについて解くと、ｄ＝２/７を得ます。

従って、DE＝９ｄ＝１８/７cmとなります。

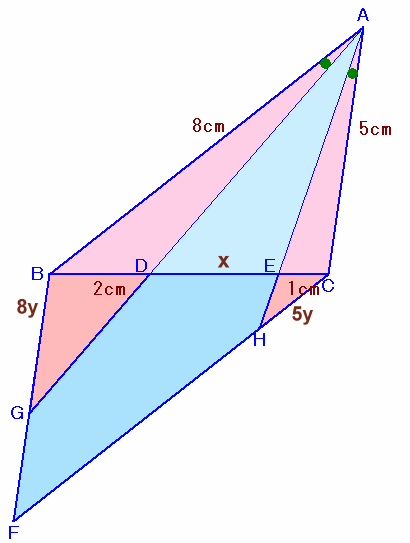
解答例４

ふじさきたつみさん、他

平行四辺形ABFCをつくり、ADの延長線とBFの交点をG、
AEの延長線とCFの交点をHとします。また、DE＝ｘとおきます。

参考図４

△ABGと△ACHは、∠BAG=∠CAH、∠ABG＝∠ACHより相似、
よって、BG：CH＝AB：AC＝８：５。

そこで、BG＝８ｙ、CH＝５ｙとおきます。

△ＡＢＥと△ＨＣＥは相似、
よって、８：５ｙ＝２＋ｘ：１　・・・　（１）

△ＡＣＤと△ＧＢＤは相似、
よって、５：８ｙ＝ｘ＋１：２　・・・　（２）

（１）÷（２）より、
　６４/２５＝２（ｘ＋２）/（ｘ＋１）

これを解いて、ｘ＝１８/７を得ます。

（その他の解法）