第３２８問の解答

問題　［場合の数］

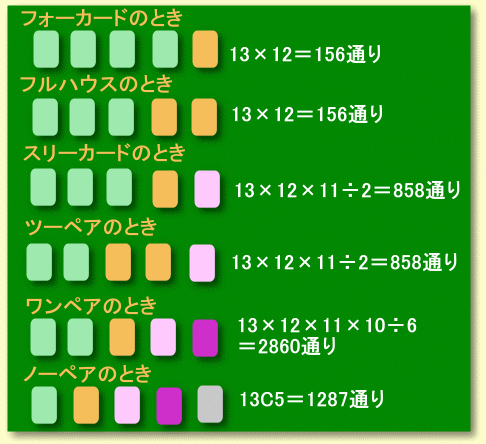
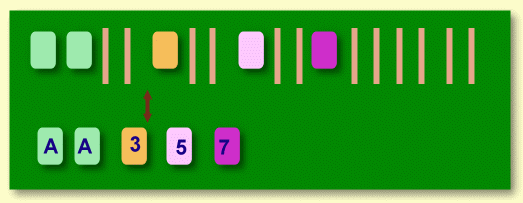
ジョーカーを除いたトランプのカード５２枚の中から５枚を取り出し、左から数の小さい順に並べます。

例えば、AAA２２、２３５９Ｋ、３７７ＪＱといった具合です。

このとき、数の並び方は何通りあるでしょうか。ただし、マークは区別しないものとします。

解答例１

長野　美光さん、Taroさん、まるケンさん、トトロ＠Ｎさん、kurosioさん、M.Hossieさん、とりやまさん、フランク長いさん、有無相生さん、saeさん、 他

参考図１

ポーカーの役によって、場合分けして数え上げると上図のようになります。

ただし、スリーカードの場合の異なる２枚のカード、ツーペアの場合のペアのカードは入れ替え可能だから２！＝２で割る必要があります。

また、ワンぺアのときは、異なる３枚のカードは入れ替え可能ですから３！＝６で割る必要があります。

よって、合計＝１５６×２＋８５８×２＋１２８７＝６１７５通りとなります。

答：　６１７５通り

以上

解答例２

CRYING DOLPHINさん、ノーザンビレッジさん、ねこやんさん、中村明海さん、ミミズクはくず耳さん、 他

トランプのカードが各種類とも際限なくあるとすると、並べ方は１３枚から５枚重複して組みあわせる場合の数となり、
　１３Ｈ５＝１3+5-1C５＝６１８８通り　となります。

実際には、このうち５カードだけは作れないので１３通りを除く必要があります。

よって、求める場合の数は、６１８８−１３＝６１７５通り。

なお、重複組み合わせは下図のように、１３＋５−１個の場所から５枚のカードを選び、残り１３−１個は枠として、
カードの場所とカードの数を対応させることで１３Ｈ５＝１3+5-1C５が成り立つことが分かります。

参考図２

（その他の解法）