第３２９問の解答

---

問題　［空間図形］

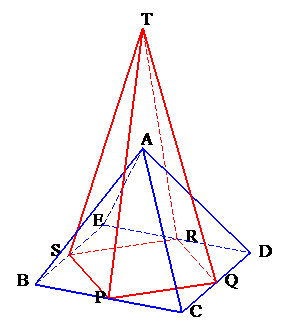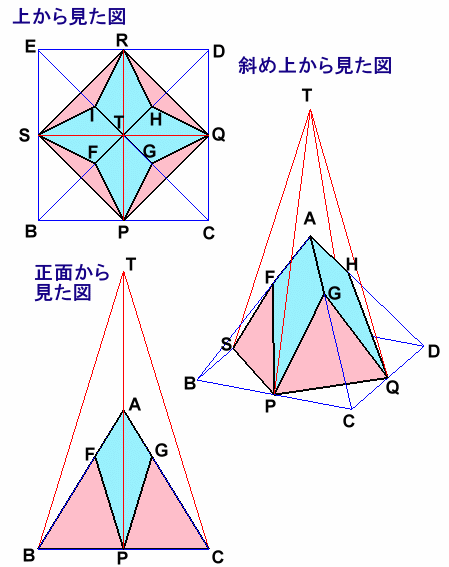
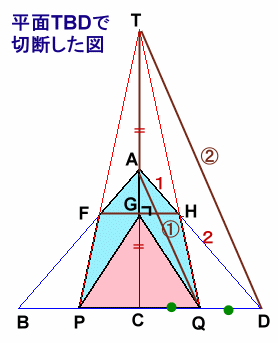
		左図のような、底面が正方形ＢＣＤＥで側面がすべて二等辺三角形である四角錐Ａ−ＢＣＤＥと、底面がＰＱＲＳで側面がすべて二等辺三角形である四角錐Ｔ−ＰＱＲＳがあります。 Ｐ、Ｑ、Ｒ、Ｓはそれぞれ辺ＢＣ、ＣＤ、ＤＥ、ＥＢの中点で、２つの四角錐は体積がともに３０cm3となっています。 このとき、四角錐Ａ−ＢＣＤＥと四角錐Ｔ−ＰＱＲＳの共通部分の体積を求めてください。

---

解答例１

長野　美光さん、CRYING DOLPHINさん、拓パパさん、あんみつさん、まるケンさん、小杉原 啓さん、トトロ＠Ｎさん、きたさんさん、ponta55555さん、フランク長いさん、ステップ　ばい　ステップさん、ミミズクはくず耳さん、M.Hossieさん、saeさん、高橋　道広さん、小西孝一さん、ますぽんさん、ねこやんさん、 他

	下図のように、求める立体は四角錐A-BCDEの４隅から三角錐を除いた形になります。 これらの頂点をF、G、H、Iとします。 三角錐の高さを求めるため、平面TBDで切断した図で考えます。 中点連結定理より、AQはTDと平行で長さは１/２。 従って、△THDと△QHAは相似で、相似比は２：１。 よって、AH：HD＝１：２。 △AGHと△ACQも相似で、相似比は１：３。 従って、GCはACの２/３。 以上から、取り除く三角錐の高さは、四角錐A−BCDEの高さの２/３で、底面の面積は１/８より、 体積は２/３×１/８＝１/１２。 よって、求める立体の体積 　＝３０×（１−１/１２×４） 　＝３０×２/３ 　＝２０cm3 となります。 答：　２０cm3 以上

---

（その他の解法）

• 積分して計算　・・・　Taroさん、有無相生さん、 他
• 座標で取り除く三角錐の高さを求める　・・・　y-iさん、他