第330問の解答
問題 [場合の数(最短経路)]
|
|
|
|
|
|
|
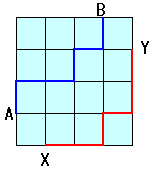 |
左図のような碁盤の目状の道路があります。 いま、A地にいるマサル君はB地に、X地にいるトモエさんはY地に、それぞれ最短距離で進むものとします。 このとき、2人が通った道筋が途中で交わったり、同じ点や道を通ったりしないような2人の進み方は何通りあるでしょうか。 |
|
|
|
|
|
|
解答例1
長野 美光さん、おかひで博士さん、sugitakukunさん、toyoさん、うっしーさん、Nonさん、Banyanyanさん、トトロ@Nさん、みっちん。さん、ponta55555さん、ミミズクはくず耳さん、をめがさん、有無相生さん、ふじさきたつみさん、ステップ ばい ステップさん、ねこやんさん、フランク長いさん、sodoさん、 他
|
|
|
|
|
|
以上 |
|
|
|
|
|
解答例2
マサルさん、CRYING DOLPHINさん、まるケンさん、 他
|
|
|
|
|
|
|
|
|
|
|
|
(その他の解法)
-
共通点を持つ経路を除く ・・・ 拓パパさん、
他
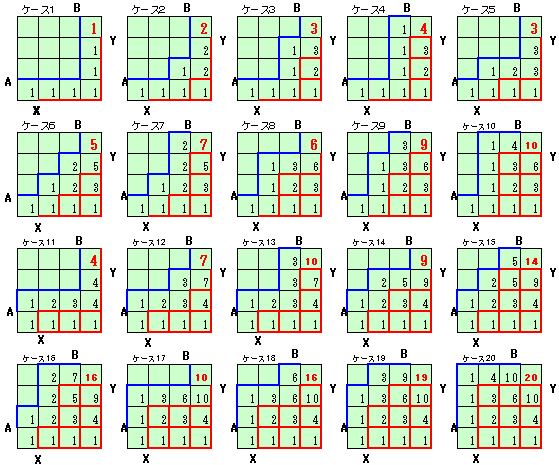
共通エリアの9点について、初めてその点で共通となる経路数225通りを、全体の400通りより除くと175通り。 - プログラムで計算 ・・・ Taroさん、高田修成さん、他