第３３１問の解答

問題［整数の性質］

０〜８までの９個の数字を並べて９ケタの整数を作ります。
この９ケタの整数から連続した３ケタの整数を以下のようにして取り出し、その和を考えます。

例）９ケタの整数が３２１０８７６５４の場合なら、
　３２１＋２１０＋１０８＋　８７＋８７６＋７６５＋６５４＝３０２１

では、このようにして作る和がもっとも大きくなるように９ケタの整数を作ると、和はいくつになるでしょうか。

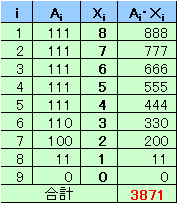
解答例１

ＡЯＯＴさん、Taroさん、高橋　道広さん、トトロ＠Ｎさん、小杉原 啓さん、ぶなしめじTZさん、ねこやんさん、ななぞうさん、N.Nishiさん、Nonさん、M.Hossieさん、小西孝一さん、ミミズクはくず耳さん、miyaさん、ふじさきたつみさん、大岡　敏幸さん、ニィ〜さん、あほあほまんさん、 他

９ケタの整数をABCDEFGHIとおきます。

求める和をSとおくと、
　S＝A×１００＋B×１１０＋（C＋D＋E＋F＋G）×１１１＋H×１１＋Ｉ
　　＝（C＋D＋E＋F＋G）×１１１＋B×１１０＋A×１００＋H×１１＋Ｉ　・・・　（１）
となります。

Ｓを最大にするには、 （１）式で係数の大きい順に数値を並べていけばいい（補題参照）ので、
　Ｃ、Ｄ、Ｅ、Ｆ、Ｇ＝８、７、６、５、４（並べ替えても可）、Ｂ＝３、Ａ＝２、Ｈ＝１、Ｉ＝０
のとき、
　Ｓ＝（８＋７＋６＋５＋４）×１１１＋３×１１０＋２×１００＋１×１１＋０
　　＝３８７１
となります。

参考図１

答：　３８７１

以上

（補題）an≧an-1≧an-2≧・・・≧a1＞０、xn＞xn-1＞xn-2＞・・・＞x1＞０のとき、
Σai・yi（ただし、yiはxiを並べ替えたもの） は、yiが大きい順に並んでいるとき最大

（証明）任意にxiを並べ替えたときのyiに対して、S0＝Σai・yiとします。

  • ステップ１ ：yn＝ｘnのときはそのまま。
    yn≠ｘnのとき、yi＝ｘnとなるのが、i＝kとするとき、
    先頭のynとyk＝ｘnを 入れ替え、このときの和をS1とする。
    　S1−S0
    ＝    （anxn＋akyn）−（anyn＋akxn）
    ＝（an−ak）（xn−yn）≧０
    　
  • ステップ２ ：yn-1＝ｘn-1のときはそのまま。
    yn-1≠ｘn-1のとき、yi＝ｘn-1となるのが、i＝k'とするとき、
    ２番目のyn-1とyk＝ｘn-1を 入れ替え、このときの和をS2とする。
    　S2−S1
    ＝    （an-1yn-1＋ak'xn-1）−（an-1xn-1＋ak'yn）
    ＝（an-1−ak'）（xn-1−yn-1）≧０

以下、同様にして、S0≦S1≦S2≦・・・≦Sn-1となります。

以上の操作で、必ずSn-1＝Σai・xiとなるので、Σai・xiが最大。

（例）
 参考図２

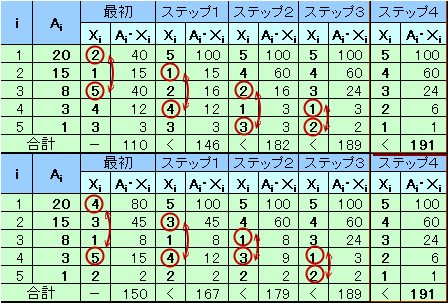
解答例２

CRYING DOLPHINさん、ステップ　ばい　ステップさん、 他

９ケタの整数をABCDEFGHIとおきます。

求める和をSとおくと、
　S＝A×１００＋B×１１０＋（C＋D＋E＋F＋G）×１１１＋H×１１＋Ｉ
　　＝（A＋B＋C＋D＋E＋F＋G＋H＋Ｉ）×１１１ −（Ｉ×１１０＋H×１００＋A×１１＋B×１）　・・・　（２）
となります。

前半部分は一定値＝３６×１１１＝３９９６なので、後半部分を最小にすればよい。

従って、Ｉ＝０、H＝１、Ａ＝２、Ｂ＝３のとき最大、
　最大値＝３９９６−（０×１１０＋１×１００＋２×１１＋３×１）
　　　　　＝３９９６−１２５
　　　　　＝３８７１

（その他の解法）