第３３２問の解答

問題［場合の数］

ある５人の生徒について、お互いの交友関係を聞いたところ、この５人の中で２つのグループが出来ていることが分かりました。

５人の生徒は、２つのグループのどちらかには必ず入っているそうです。

このとき、２つのグループのメンバー構成の組み合わせは何通り考えられるでしょうか。

ただし、両方のグループに入っている生徒がいてもよいものとします。
なお、１人だけのグループがあってもかまいませが、５人のグループはないものとします。

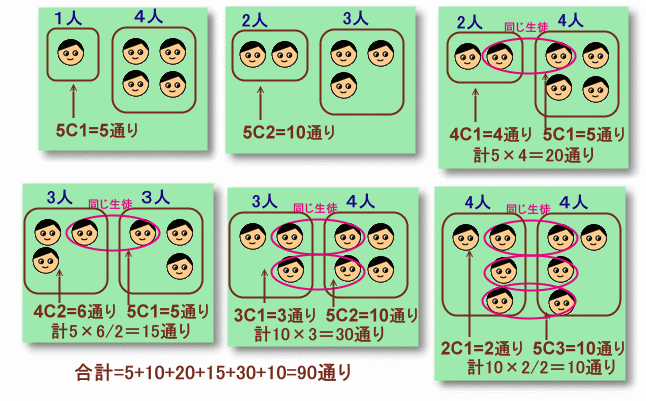
解答例１

ミミズクはくず耳さん、まるケンさん、N.Nishiさん、前田先生＠P進学院さん、有無相生さん、航介さん、ふじさきたつみさん、ももちゃんさん、 他

グループの人数で場合分けすると、
　（１、４）、（２、３）、（２、４）、（３、３）、（３、４）、（４、４）
の６通りになります。

参考図１

  • （１、４）のとき：
    ５人から１人を選べば残りの４人は自動的に決まるので、5Ｃ1＝５通り
    　

  • （２、３）のとき：
    ５人から２人を選べば残りの３人は自動的に決まるので、5Ｃ2＝１０通り
    　

  • （２、４）のとき：
    両方のグループに入っている生徒が１人いるので、これを選ぶのは5Ｃ1＝５通り、
    残り４人から１人を選べば後の３人は自動的に決まるので、4Ｃ1＝４通り、
    　合計：５×４＝２０通り
    　

  • （３、３）のとき：
    両方のグループに入っている生徒が１人いるので、これを選ぶのは5Ｃ1＝５通り、
    残り４人から２人を選べば後の２人は自動的に決まるので、4Ｃ2＝６通り、
    重複を省いて、合計：５×６／２＝１５通り
    　

  • （３、４）のとき：
    両方のグループに入っている生徒が２人いるので、これを選ぶのは5Ｃ2＝１０通り、
    残り３人から１人を選べば後の２人は自動的に決まるので、3Ｃ1＝３通り、
    　合計：１０×３＝３０通り
    　

  • （４、４）のとき：
    両方のグループに入っている生徒が３人いるので、これを選ぶのは5Ｃ3＝１０通り、
    残り２人から１人を選べば後の１人は自動的に決まるので、2Ｃ1＝２通り、
    重複を省いて、合計：１０×２／２＝１０通り

従って、合計＝５＋１０＋２０＋１５＋３０＋１０＝９０通りとなります。

答：　９０通り

以上

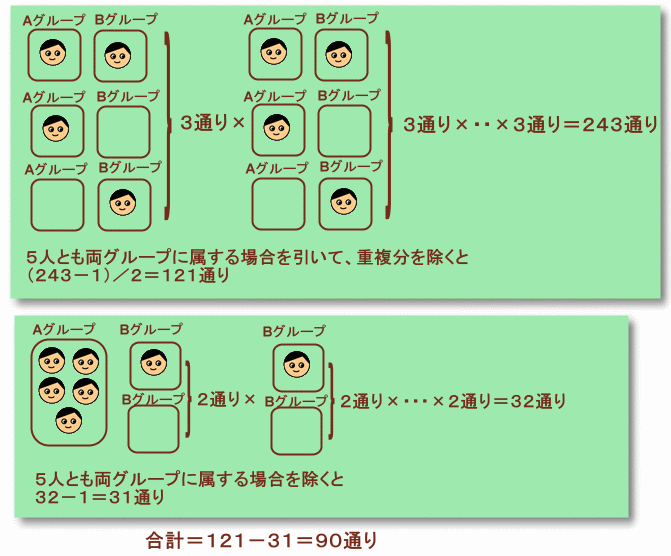
解答例２

マサルさん、中村明海さん、フランク長いさん、M.Hossieさん、ねこやんさん、小西孝一さん、をめがさん、品川コータさん、 他

参考図２

２つのグループをA、Bとします。

各生徒は、

  • A、B両方に入っている

  • Aのみ入っている

  • Bのみ入っている

の３通り考えられるので、５人の生徒では３5＝３４３通り。

この中には、５人とも両グループに入っているケース１通りを除く必要があり、
また実際にはA、Bのグループは区別されないので、この重複を除くと、
　（３４３−１）／２＝１２１通り
となります。

さらに、５人のグループができている場合として、
もう一方のグループに各生徒が、入る、入らないの２通りづつあるので、
　２5＝３２通り
このうち、両グループとも５人のケースは既に除外しているので、
　３２−１＝３１通り

従って、合計では１２１−３１＝９０通りとなります。

（その他の解法）