第３３３問の解答

問題［空間図形］

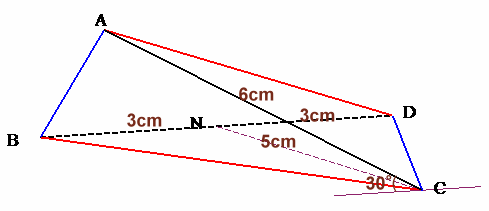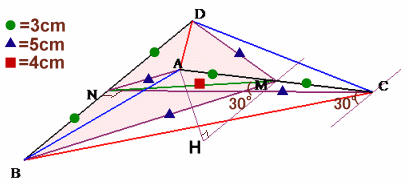
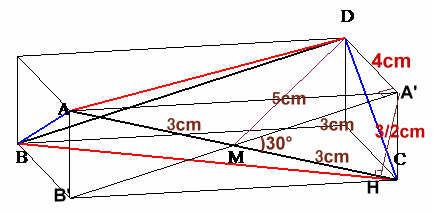
問題図 左図のような、ＡＣ＝ＢＤ＝６cm、ＡＢ＝ＣＤ、ＡＤ＝ＢＣの三角錐ＡＢＣＤがあります。

頂点Cと辺BDの中点Nを結ぶと５cmになります。また、点Ｃを通り辺ＢＤに平行な直線をひくと、辺ＡＣと３０°で交わります。

このとき、三角錐ＡＢＣＤの体積を求めてください。

　

解答例１

トトロ＠Ｎさん、フランク長いさん、takaisaさん、 他

辺ACの中点をM、辺BDの中点をNとします。

参考図１

△MDB、△NCAは、どちらも底辺が６cm、斜辺が５cmの二等辺三角形。
よって、△MDN、△MBN、△NCM、△NAMは、全て３辺が３：４：５の直角三角形となる。

従って、MN＝４cm、△ＭＤＮ＝１/２×BD×MN＝１/２×６×４＝１２cm2。

ここで、頂点Aから、Mを通ってDBに平行な直線に下ろした垂線の足をHとします。

DBとMHは平行で、ANとDBが直交、従ってMHとMNが直交、かつMNはACと直交、
従って、三垂線の定理より、HはAから平面MDBに下ろした垂線の足ともなります。

∠ＡＭＨ＝３０°より、ＡＨ＝ＡＭ×１/２＝３/２cm。

さて、三角錐ＡＢＣＤを平面ＭＤＢで分割すると、ＭはＡＣの中点だから、
分割してできる２つの三角錐の体積は等しい。

従って、三角錐ABCD
　＝三角錐ＡＭＤＢ×２
　＝１/３×△ＭＤＢ×ＡＨ×２
　＝１/３×１２×３/２×２
　＝１２cm3
となります。
　

答：　１２cm3

以上

解答例２

中村明海さん、長野　美光さん、CRYING DOLPHINさん、クララさん、ねこやんさん、うっしーさん、ミミズクはくず耳さん、 他

三角錐ABCDの４面は全て合同な三角形なので、
もし、これらが鋭角三角形ならば下図のように直方体にすっぽり収めることができます。(注)

参考図２

DAは平面AB'CA'と直交するので、∠DA'M＝９０°、
よって、△DMA'は３辺が３：４：５の直角三角形となります。
従って、DA'＝４cm。

DBとA'Mは平行なので、題意より、ACとA'Mは３０°で交差します。

よって、A'からACに下ろした垂線の足をHとすると、
　A'H＝AM×１/２＝３/２cm。

従って、長方形AB'CA'＝１/２×AC×A'H×２＝６×３/２＝９cm2。
よって、直方体の体積V＝４×９＝３６cm2。

さて、三角錐ABCDは直方体から４個の三角錐を除いたものなので、
三角錐ABCD＝V−１/６×V×４＝V×１/３＝３６×１/３＝１２cm2となります。

（注）
三角形の３辺の長さをａ、ｂ、ｃとします。
直方体の横、縦、高さをｘ、ｙ、ｚとすると、
　ｘ2＋ｙ2＝ａ2　・・・　（１）
　ｙ2＋ｚ2＝ｂ2　・・・　（２）
　ｚ2＋ｘ2＝ｃ2　・・・　（３）
が成り立つ必要があります。

｛（１）＋（２）＋（３）｝／２より、
　ｘ2＋ｙ2＋ｚ2＝（ａ2＋ｂ2＋ｃ2）／２　・・・　（４）

（４）−（２）より、ｘ2＝（ａ2−ｂ2＋ｃ2）/２、
（４）−（３）より、ｙ2＝（ａ2＋ｂ2−ｃ2）/２、
（４）−（１）より、ｚ2＝（−ａ2＋ｂ2＋ｃ2）/２　・・・　（５）

（５）を満たすａ、ｂ、ｃが存在するには、三角形が鋭角三角形であることが必要かつ十分。

よって、三角形が鋭角三角形ならば、三角錐が収まるような直方体が存在し、
また（５）より、そのような直方体の大きさは１通りしかないことが分かります。　

（その他の解法）