第３３５問の解答

問題［平面図形］

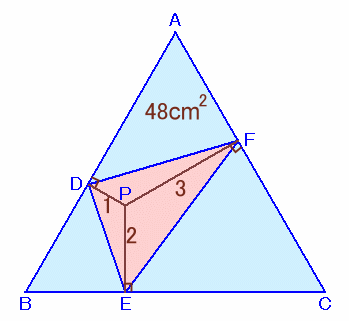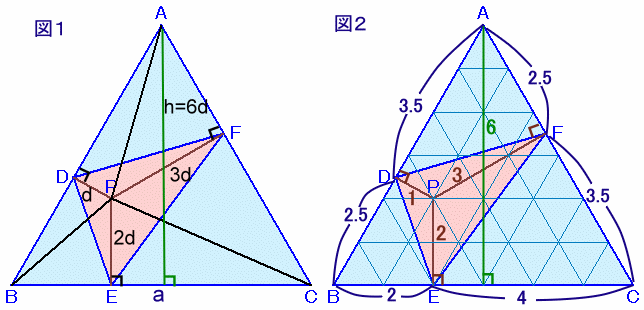
問題図 左図のような、面積が４８cm2の正三角形ＡＢＣがあります。

いま、正三角形の内部に点Ｐをとり、Ｐから辺ＡＢ、辺ＢＣ、辺ＣＡに降ろした垂線の足をそれぞれＤ、Ｅ、Ｆとします。その結果、ＰＤ：ＰＥ：ＰＦ＝１：２：３となりました。

このとき、三角形ＤＥＦの面積を求めてください。
　

解答例１

まるケンさん、Taroさん、中村明海さん、ｋｏｓｕｋｅさん、をめがさん、おりくんさん、 他

正三角形ＡＢＣの長さ、高さをaおよびhとします。

参考図１

△ABC＝△PAB＋△PBC＋△PCA　・・・　（１）
1/2×a×h＝1/2×a×d＋1/2×a×２d＋1/2×a×３d
1/2×a×h＝1/2×a×（d＋２d＋３d）

従って、h＝６dと分かります。

よって、正三角形ABCを３６個の小正三角形に分割すると、
PはAB、BC、CAより高さが１、２、３の位置にあることから図２のようになります。

よって、
　AD：DB＝３．５：２．５＝７：５、
　BE：EC＝２：４、
　CF：FA＝３．５：２．５＝７：５。

小正三角形の面積を１とすると、
　△ADF＝２．５×３．５＝３５/４、
　△BED＝２．５×２＝５、
　△CFE＝４×３．５＝１４

よって、△DEF＝３６−（３５/４＋５＋１４）＝３３/４。

小正三角形の面積＝４８/３６cm2だから、
　△DEF＝３３/４×４８/３６＝１１cm2
となります。

答：　１１cm2

以上

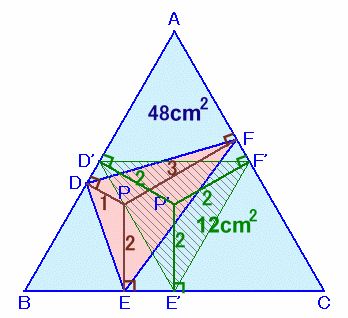
解答例２

ステップ　ばい　ステップさん、ふじさきたつみさん、ミミズクはくず耳さん、ドルミカムさん、小学名探偵さん、 他

正三角形ＡＢＣの中心をP'とし、P'から下ろした垂線の足D'、E'、F'とします。
これらはAB、BC、CAの中点となります。

参考図２

△D'E'F'＝△ABC×１/４＝４８×１/４＝１２cm2。

△PDE、△PEF、△PFD、および△P'D'E'、△P'E'F'、△P'F'D'は、
いずれも挟まれる角度が１２０度と共通だから、面積は挟む２辺の長さの積に比例します。

従って、
　△DEF：△D'E'F'＝（１×２＋２×３＋３×１）：（２×２＋２×２＋２×２）＝１１：１２、
よって、
　△DEF＝△D'E'F'×１１/１２＝１２×１１/１２＝１１cm2。

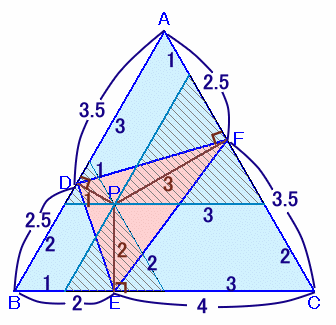
解答例３

CRYING DOLPHINさん、ponta55555さん、Banyanyanさん、ねこやんさん、 他

Pを通り各辺と平行に直線を引きます。

参考図３

すると、PD、PE、PFを高さとする３つの正三角形ができます。
　各辺の長さの比＝PD：PE：PF＝１：２：３。

よって、
　AD：DB＝（３＋０．５）：（０．５＋２）＝７：５、
　BE：EC＝（１＋１）：（１＋３）＝２：４、
　CF：FA＝（２＋１．５）：（１．５＋１）＝７：５。

以下、解答例１と同様。

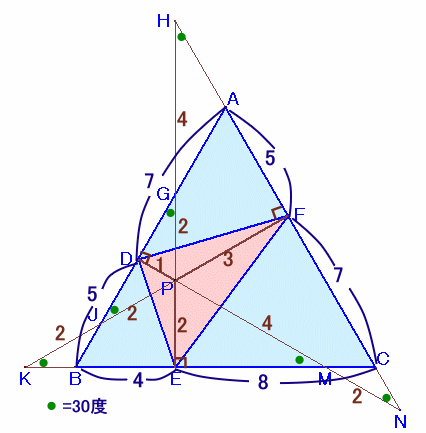
解答例４

フランク長いさん、 他

EPとABの交点をG、およびCAとの交点をH、
FPとABの交点をJ、およびCBとの交点をK、
DPとBCの交点をM、およびACとの交点をN、とします。

参考図４

△GPD、△HPFは、いずれも頂角が３０度の直角三角形。

従って、PDの長さを１とおくと、
　GP＝PD×２＝２
　HP＝PF×２＝６。

また、△GBE、△HCEも、頂角が３０度の直角三角形。

よって、
　BE：EC＝GE：HE＝４：８。

同様にして、
　CF：FA＝KF：JF＝７：５
　AD：DB＝ND：MD＝７：５。

以下、解答例１と同様。

（その他の解法）