第３３６問の解答

問題［平面図形］

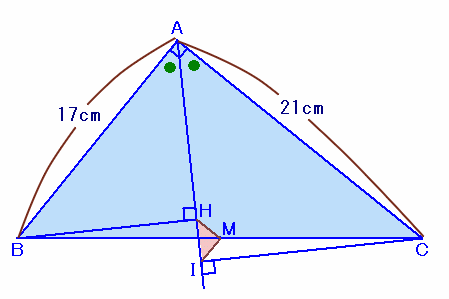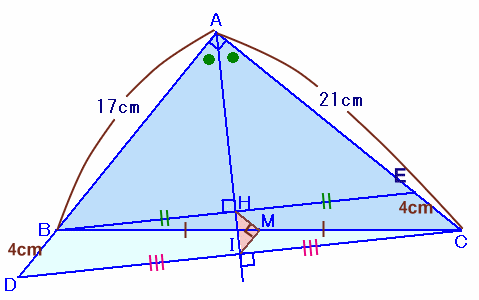
問題図 左図のような、ＡＢ＝１７cm、ＡＣ＝２１cm、∠Ａ＝９０度の直角三角形ＡＢＣがあります。

いま、∠Ａの二等分線に頂点Ｂ、Ｃから下ろした垂線の足をそれぞれＨ、Ｉとします。また、辺ＢＣの中点をＭとします。

このとき、△ＨＭＩの面積を求めてください。
　

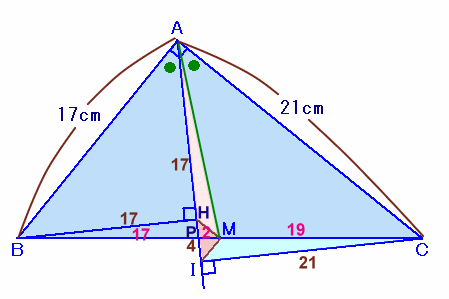
解答例１

CRYING DOLPHINさん、小杉原 啓さん、拓パパさん、たかまつ　ろろさん、takaisaさん、ゆんななこさん、ふじさきたつみさん、M.Hossieさん、他

ＢHの延長線とACの交点をEとし、CIの延長線とABの延長線の交点をDとします。

参考図１

△ABEはAB=AEの直角２等辺三角形で、HはBEの中点となります。

よって、△EBCで中点連結定理により、
　HMとECは平行、HM＝EC×１/２＝２cm　・・・　（１）
となります。

また、△DCBで中点連結定理により、
　IMとBDは平行、MI＝BD×１/２＝２cm　・・・　（２）
となります。

ABとACは直交しているので、（１）、（２）より、HMとMIも直交。

よって、△HMIは直角二等辺三角形となります。
　△HMI＝HM×MI×１/２＝２×２×１/２＝２cm2
となります。　

答：　２cm2

以上

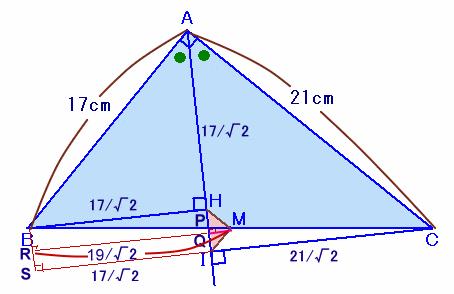
解答例２

クララさん、ねこやんさん、トトロ＠Ｎさん、フランク長いさん、 他

BCとAIの交点をPとします。

参考図２

△AICは、AI＝CIの二等辺直角三角形で斜辺の長さ＝２１cm、
従って、
　△AIC＝（２１/２）2＝２１×２１/４cm2。

AIは∠BACの二等分線だから、
　BP：PC＝AB：AC＝１７：２１

よって、PM：ＰC＝２：２１。

従って、
　△ＡＩＭ＝△ＡＩＣ×２/２１＝２１/２cm2。

また、△AＨＢは、AＨ＝ＢＨの二等辺直角三角形で斜辺の長さ＝１７cm。

従って、ＡＨ：ＡＩ＝１７：２１、ＰＩ：ＡＩ＝４：２１。

よって、
　△ＰＭＩ＝△ＡＩＭ×４/２１＝２１/２×４/２１＝２cm2。

解答例３

高田修成さん、ＩＣさん、あほあほまんさん、あんみつさん、 他

ＢＳをＡＩと平行な直線、ＭＲ、IＳをＣＩと平行な直線とします。

参考図３

△ＡＨＢ、△ＡＩＣは直角二等辺三角形だから、
　ＢＨ＝ＡＨ＝１７/√２cm、
　ＡＩ＝ＣＩ＝２１/√２cm。

よって、ＨＩ＝ＡＩ−ＡＨ＝４/√２cm。

ＢＲＱＰ、ＲＳＩＱは平行四辺形だから、
　ＲＱ＝ＳＩ＝ＢＨ＝１７/√２cm。

△ＣＢＳで中点連結定理より、
　ＲＭ＝ＳＣ×１/２＝１９/√２cm。

よって、
　ＱＭ＝ＲＭ−ＲＱ＝２/√２cm。

従って、
　△ＨＭＩ＝１/２×ＰＩ×ＱＭ
　　　　　＝１/２×４/√２cm×２/√２cm
　　　　　＝２ｃｍ2。

（その他の解法）