第３３７問の解答

問題［場合の数、剰余］

１〜１３までのカードが１枚ずつあります。

これらの中から４枚を同時に取り出すとき、４枚のカードに書かれた数の合計が１３の倍数になるような取り出し方は何通りあるでしょうか。

解答例１

トトロ＠Ｎさん、sugitakukunさん、ミミズクはくず耳さん、ねこやんさん、あほあほまんさん、ステップ　ばい　ステップさん、M.Hossieさん、航介さん、フランク長いさん、富山清風さん、他多数

４枚のカードの数を小さい順にa、b、c、dとして数え上げていきます。

まず、１〜１１から異なる２個の数を選び小さい方からa、bとします。

  • （a、b）＝（１、２）のとき　・・・　a＋b＝３だから、和が１３の倍数となるのは、c＋d＝１０または２３
    よって、（c、d）＝（３、７）、（４、６）、（１０、１３）、（１１、１２）
  • （a、b）＝（１、３）のとき　・・・　a＋b＝４だから、和が１３の倍数となるのは、c＋d＝９または２２
    よって、（c、d）＝（４、５）、（９、１３）、（１０、１２）

以下、同様にして下表の結果を得ます。

参考図１

よって、和が１３の倍数となるのは、合計５５通りとなります。
　

答：　５５通り

以上

解答例２

数楽者さん、Miki Sugimotoさん、kotaeさん、 他

一般化して考えます。

（補題）
２つの自然数n>mが互いに素の場合、１〜nの数から異なるm個の数を同時に選んだとき、
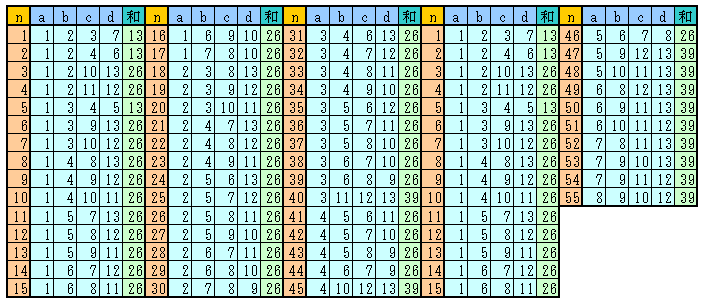
これらの和をnで割った余りの個数は全て同じ。（本問では、n＝１３、m＝４の場合）

  1. １〜nの数から異なるm個の数を同時に選ぶ選び方は、全部でnCm通りあります。
    まず、これがnの倍数であることを示します。

    n-1Cm-1＝(n-1)！/（n-m）！(m-1)！
    　　　＝{n！/（n-m）！m！}×m/n
    　　　    ＝nCm×m/n

    n    とmは互いに素だから、nCmはnで割り切れる。・・・（１）
    　
  2. １〜nの数から異なるm個の数を同時に選ぶ選び方全体を｛G｝として、
    これを次のようにn個のグループ分けします。

    ｛G｝から任意にG0＝（a1、a2、・・、am）を取り出します。
    k＝0〜n-1に対し、Gk＝（a1＋k、a2＋k、・・、am＋k）とし、
    ap    ＋kがnを超えた場合はap＋k−nに置き換えることとします。

参考図２

すると、Gkの各数は1〜nとなります。　・・・（２）
これらの和をsk、およびskをnで割った余りをｒkとすると、ｒkは全て異なります。・・・（３）

なぜなら、もしｒp＝ｒq（ただし、p<q）と仮定すると、sq−spはnの倍数となりますが、
　sq−sp＝｛（a1＋q）＋（a2＋q）＋・・＋（am＋q）｝-｛（a1＋p）＋（a2＋p）＋・・＋（am＋p）｝
　　　　　＝（a1＋a2＋・・＋am＋m×q）-（a1＋a2＋・・＋am＋m×p）
　　　　　＝m×q-m×p
　　　　　＝m×（q−p）
となり、mはnと互いに素で、しかも、0<q−p<nより、sq−spがnの倍数と矛盾します。

また、Gkについても全て異なります。　・・・（４）
もし、Gp＝Gq（ただし、p<q）と仮定すると、ｒp＝ｒqとなって矛盾するからです。

従って、｛G0、G1、・・・、Gn-1｝はn個の相異なる｛G｝の要素となります。

また、Gn＝（a1＋n-n、a2＋n-n、・・、am＋n-n）＝G0となることから、
このグループのどの要素を最初のG0としても同じグループになることが分かります。　・・・（５）

従って、別のグループG'nの各要素は全てGn要素と異なることになります。

以上から補題が成り立つことが示されました。

よって、和をnで割った余りの個数は全て同じだから、ｎCm/n通りとなります。

とくに本問では、13C4/１３＝７１５/１３＝５５通りとなります。

　

(参考)n＝８、m＝３の場合のグループ化の例

参考図３
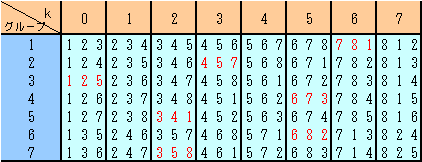
（注）赤字：和がn＝８の倍数
　

（その他の解法）