第３３８問の解答

問題［平面図形］

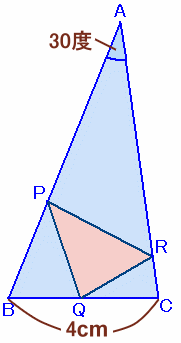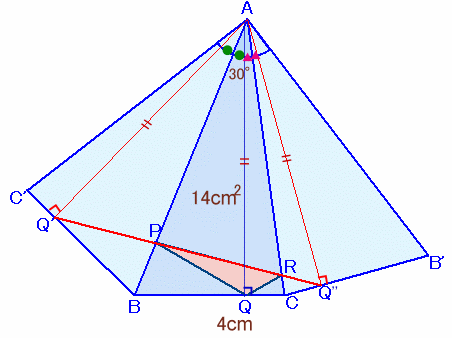
問題図 左図のような、面積が１４cm2、∠Ａ＝３０°、辺ＢＣ＝４cmの△ＡＢＣがあり、∠Ｂ、∠Ｃの大きさは９０°未満になっています。

いま、辺ＡＢ上に点Ｐ、辺ＢＣ上に点Ｑ、辺ＣＡ上に点Ｒをとりました。

△ＰＱＲの周の長さを最も短くなるようにするとき、その長さを求めてください。

解答例１

CRYING DOLPHINさん、トトロ＠Ｎさん、ステップ　ばい　ステップさん、拓パパさん、あほあほまんさん、M.Hossieさん、ねこやんさん、ふじさきたつみさん、ミミズクはくず耳さん、大岡　敏幸さん、他多数

△ＡＢＣをＡＢを軸に折り返したものを△ＡＢＣ'、ＡＣを軸に折り返したものを△ＡＢ'Ｃ、
△PQRの周をｄとします。

参考図１

ＰＱ'＝ＰＱ、Ｑ''Ｒ＝ＱＲより、ｄ＝ＰＱ＋ＱＲ＋ＲＰ＝Ｑ'Ｐ＋ＰＲ＋ＲＱ''

従って、Ｑを固定したとき、△ＰＱＲの周が最も短くなるのは、
Ｑ'、Ｐ、Ｒ、Ｑ''が一直線上に並ぶときです。

さて、ＡＱ'＝ＡＱ''＝ＡＱより、△ＡＱ'Ｑ''は二等辺三角形。

また、∠Q'AB＝∠QAB、∠Q''AC＝∠QAC、
従って、∠Q'AQ''＝∠BAC×２＝６０°。

よって、△ＡＱ'Ｑ''は正三角形となりますので、ｄ＝Q'Q''＝AQ。

従って、△ＰＱＲの周が最も短くなるのは、AQが最小となるときです。
このとき、QはAからBCに下ろした垂線の足となります。

△ABC＝１/２×AQ×BC

よって、ｄの最小値は、
　AQ＝△ABC×２／BC＝１４×２／４＝７cm
となります。

答：　７cm

以上

（その他の解法）