第３３９問の解答

問題［平面図形］

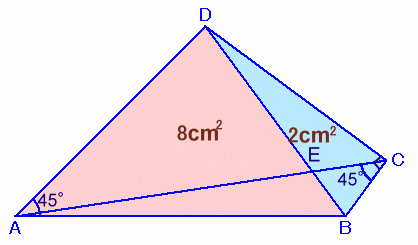問題図 左図のような、∠ＢＡＤ＝４５°、∠ＢＣＤ＝９０°の四角形ＡＢＣＤがあります。

いま、頂点Ａと頂点Ｃを結んだところ、∠ＡＣＢ＝４５°でした。また、△ＡＢＤの面積は８cm2、△ＢＣＤの面積は２cm2であるそうです。また、ＡＣとＢＤの交点をＥとします。

このとき、ＡＥの長さを求めてください。

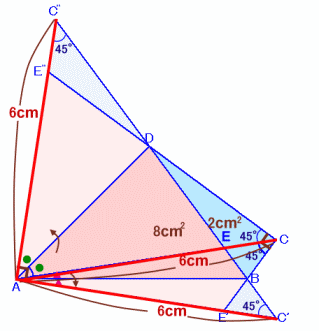
解答例１

CRYING DOLPHINさん、Banyanyanさん、maruhagedonさん、ステップ　ばい　ステップさん、鉄老さん、他

ＡＢを軸に△ＡＢＣを折り返したものを△ＡＢＣ'、ＡＣを軸に△ACDを折り返したものを△ＡＣ''Dとします。

参考図１

∠C''AC'＝∠C''AD＋∠DAC＋∠CAB＋∠BAC'
　　　　＝（∠DAC＋∠CAB）×２
　　　　＝４５°×２
　　　　＝９０°
および、AC''＝AC'＝ACより、△AC''C'は、直角二等辺三角形となります。

ところが、∠AC''D＝∠ACD＝４５°、∠AC'B＝∠ACB＝４５°、
従って、C''、D、B、C'は、一直線上に並んでいます。

△AC''C'＝（△C''AD＋△BA'C'）＋△ABD
　　　　　＝（△ABD＋△BCD）＋△ABD
　　　　　＝８＋２＋８
　　　　　＝１８cm2

従って、△AC''C'は直角二等辺三角形だから、
　１辺の長さは、面積が１８×２＝３６cm2の正方形の１辺に等しい。

よって、AC＝AC''＝AC'＝６cmとなります。

AE：EC＝△ABD：△BCD＝８：２＝４：１。

従って、AE＝AC×４/５＝６×０．８＝４．８cmとなります。

答：　４．８cm

以上

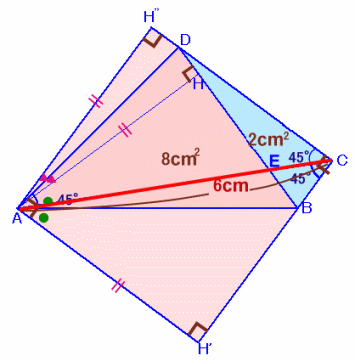
解答例２

角さん、ねこやんさん、萬田銀次郎さん、中村明海さん、ふじさきたつみさん、あんみつさん、トトロ＠Ｎさん、 他

頂点Aから辺BD、BCおよびCDに下ろした垂線の足をH、H'、H''とします。

参考図２

∠H'、∠C、∠H''とも直角だから、∠Aも直角になります。
従って、四角形AH'CH''は長方形になります。

また、∠ACH'＝∠ACH''＝４５°より、長方形AH'CH''は、正方形となります。

さて、ABを軸に△ABH'を、ADを軸に△ADH''を折り返します。

すると、∠DBH'＋∠DAH''＝∠A−∠DBA＝４５°＝∠DBA、
従って、辺AH'と辺AH''は重なります。

また、AH'＝AH''（正方形だから）より、頂点H'とH''も一致します。

ところが、∠H'＝∠H''＝直角だから、この一致する点は辺BD上にあり、
辺AH'と辺BDが直交することから、この点はHと一致することとなります。

従って、
　正方形の面積＝△ABD×２＋△BCD＝８×２＋２＝１８cm2。

よって、対角線の長さAC＝６cmとなります。

以下、解答例１と同様にして、AE＝AC×４/５＝６×０．８＝４．８cmとなります。

（その他の解法）