第３４２問の解答

問題［場合の数］

「ジャンケンの帝王」と呼ばれるマサルさんは、「連敗などをしない」という伝説の男です。

つまり、「勝ち」の次の勝負は、「勝ち」「負け」「あいこ」のどれかになりますが、
　「負け」や「あいこ」の次の勝負には必ず「勝ち」ます。

あるときマサルさんが、７人の人と連続でジャンケン勝負をしました。

このときのマサルさんの勝負の勝敗表は、勝ちを◎、あいこを▲、負けを×とすると、例え ば

　　◎→◎→×→◎→▲→◎→◎

のようになります。では、マサルさんの勝敗表は何通り考えられるでしょうか。

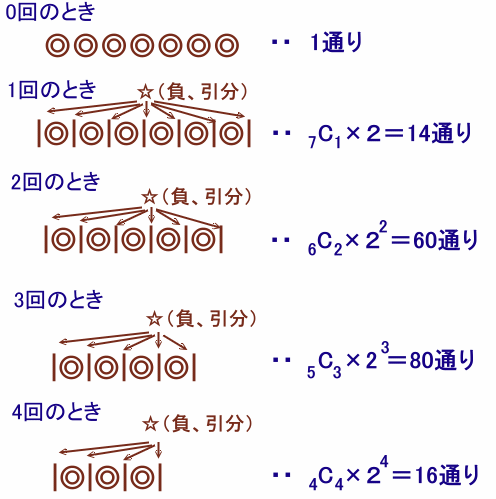
解答例１

小杉原 啓さん、Toru Fukatsuさん、CRYING DOLPHINさん、るてみいなさん、フランク長いさん、ミミズクはくず耳さん、有無相生さん、M.Hossieさん、長野　美光さん、らんまさん、Banyanyanさん、kazayaさん、Taroさん、ねこやんさん、つく子さん、tomoさん、他

n回勝負したときの場合の数をFnとして、nに関する漸化式を考えます。

参考図１

  • n＝１のとき、勝、負、引分の３通り、よってF1＝１。

  • n＝2のとき、(勝、勝）、（勝、負）、（勝、引分）、（負、勝）、（引分、勝）の５通り、よってF2＝５。

n≧３のとき、

  • 最初が勝のとき　・・・　　２回目以降はFn-1通り

  • 最初が負、引分のとき　・・・
    　２回目は必ず勝であり、３回目以降はFn-2通り

より、
　Fn＝Fn-1＋２Fn-2 ・・・（１）
が得られます。

従って、順次

  • F3＝F2＋２F1＝５＋２×３＝１１

  • F4＝F3＋２F2＝１１＋２×５＝２１

  • F5＝F4＋２F3＝２１＋２×１１＝４３

  • F6＝F5＋２F4＝４３＋２×２１＝８５

  • F7＝F6＋２F5＝８５＋２×４３＝１７１

となりますので、７回勝負ではF7＝１７１通りとなります。

なお、一般式は、（１）より、x2−x−２＝０の根x＝２、−１を用いて
　Fn＝ａ×２n-1＋ｂ×（−１）n-1
と表されます。

ａ、ｂは、F1＝ａ＋ｂ＝３、F2＝２ａ−ｂ＝５を解いて、ａ＝８/３、ｂ＝１/３となりますので、
　Fn＝８/３×２n-1＋１/３×（−１）n-1
となります。

答：　１７１通り

以上

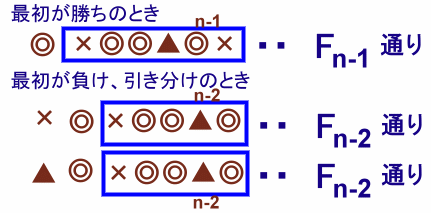
解答例２

遠い山のぽきょぽんさん、ponta55555さん、トトロ＠Ｎさん、Banyanyanさん、大岡　敏幸さん、 他

負、引分の回数によって場合分けして数えます。

参考図２

  • ０回のとき　・・・　７回全て勝つのは、１通り

  • １回のとき　・・・　６回の勝の間（両端を含む）７個所のうち１個所が負、引 分
    なので、７Ｃ１×２＝１４通り

  • ２回のとき　・・・　５回の勝の間（両端を含む）６個所のうち２個所が負、引 分
    なので、6Ｃ2×２2＝６０通り

  • ３回のとき　・・・　４回の勝の間（両端を含む）５個所のうち３個所が負、引 分
    なので、5Ｃ3×２3＝８０通り

  • ４回のとき　・・・　３回の勝の間（両端を含む）４個所のうち４個所が負、引 分
    なので、4Ｃ4×２4＝１６通り

従って、合計＝１＋１４＋６０＋８０＋１６＝１７１通りとなります。

（その他の解法）