第３４３問の解答

問題［平面図形］

問題図 左図のような正三角形ＡＢＣがあり、辺ＢＣを一辺とする正方形の面積は７２cm2となっています。

いま、この正三角形の各頂点を中心とする円（半径は３つとも同じです）を描いたところ、上の図のように３点Ｄ、Ｅ、Ｆで交わり、∠ＥＡＦ＝３０°となりました。

このとき、図中のピンク色の部分（正三角形ＡＢＣから、円弧ＤＥ、ＥＦ、ＦＤで囲まれた図形を除いた部分）の面積を求めてください。ただし、円周率は３.１４とします。

　

解答例１

おりくんさん、たけちゃんさん、フランク長いさん、ミミズクはくず耳さん、ふじさきたつみさん、中村明海さん、わっきさん、他

下図のように求める図形を３分割します。

参考図１

△ＡＥＣについて、ＡＥ＝ＥＣで∠ＥＡＣ＝∠ＥＣＡ＝４５°より、
△ＡＥＣは直角二等辺三角形となります。

斜辺ＡＣは面積が７２cm2の正方形の一辺だから、
ＡＥ＝ＥＣを一辺とする正方形の面積は半分の３６cm2。
よって、ＡＥ＝ＥＣ＝６ｃｍ。

従って、
　ＡＦＥＣ
＝△ＡＥＣ−扇形ＡＥＦ
＝１/２×６×６−３．１４×６×６×３０/３６０
＝１８−９．４２
＝８．５８cm2

よって、求める図形の面積＝８．５８×３＝２５．７４cm2

答：　２５．７４cm2

以上

解答例２

トトロ＠Ｎさん、ねこやんさん、小金井のチンジャラさん、mohyamaさん、あいびぶさん、kasamaさん、 他

下図のように求める図形を３分割します。

参考図２

解答例１と同様にして円の半径は６ｃｍ。

分割した図形（例えば緑色の部分）は、
角度が６０度の扇形からどんぐり型の図形ＤＥ'F'を除いたものになります。

前者の面積＝３．１４×６×６×６０/３６０＝１８．８４cm2。
後者の面積＝図形DE'H×２＝（角度４５度の扇形−△DHC）×２
　　　　　　　＝３．１４×６×６×４５/３６０×２−３×３×２
　　　　　　　＝２８．２６−１８＝１０．２６cm2。

よって、
求める図形の面積＝（１８．８４−１０．２６）×３＝８．５８×３＝２５．７４cm2。

解答例３

CRYING DOLPHINさん、 他

下図のように求める図形を３分割します。

参考図３

分割した図形（例えばEBCF）は、等脚台形EBCFから弓形EFを除いたものになっている。

等脚台形EBCFを△EBCと△EFCに分割し、右図のように組み合わせると、
C、F、C'は∠Ｃ'Ｂ'Ｅ＋∠ＥＦＣ＝４５＋１３５＝１８０度だから一直線上に並びます。

また、ＥＣ'＝ＥＣ＝６cmより、△C'ECは底角が１５度の二等辺三角形となり、
　△C'EC＝１/２×６×３＝９cm2。

また、弓形EF
　＝扇形AEF−△AEF
　＝３．１４×６×６×３０/３６０−１/２×６×３
　＝９．４２−９
　＝０．４２cm2。

よって、求める面積＝（９−０．４２）×３＝８．５８×３＝２５．７４cm2。

解答例４

Taroさん、takuさん、sugitakukunさん、あほあほまんさん、takaisaさん、ponta55555さん、ハラギャーテイさん、小西孝一さん、有無相生さん、大岡　敏幸さん、 他

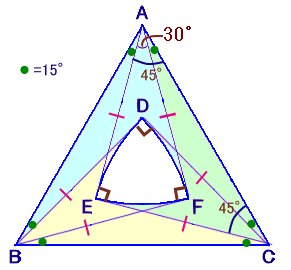
△ABCの一辺の長さをa、AE＝r、EF＝bとおき、これらの長さを実際に求めて計算します。

参考図４

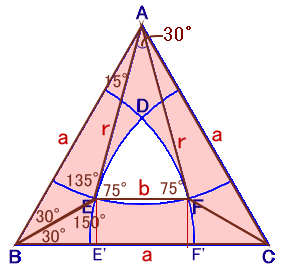
aは面積７２cm2の正方形の一辺だから、a2＝７２、
よって、a＝√７２＝６√２cm。

△AEBについて正弦定理より、
　a/sin135°＝r/sin30°
よって、
　ｒ＝a×sin30°/sin135°＝６√２×(１/２)／(√２/２)＝６cm。

△AEFについて余弦定理より、
　EF2＝AE2＋AF2−２AE・AF・cos30°
　b2＝r2＋r2−２r・r・cos30°＝r2・（２−√３）＝３６×（２−√３）

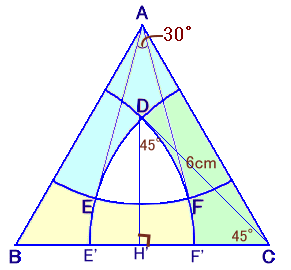
　求める面積
＝△ABC−△DEF−弓形EF×３
＝√３/４×ａ2−√３/４×ｂ2−（πｒ2×３０/３６０−1/2×r2・sin３０°）×３
＝√３/４×７２−√３/４×３６×（２−√３）−（３．１４×６2×１/４−1/2×６2×1/2）×３
＝√３×１/４×√３×３６−（３．１４×９−９）×３
＝５４−２８．２６
＝２５．７４cm2。

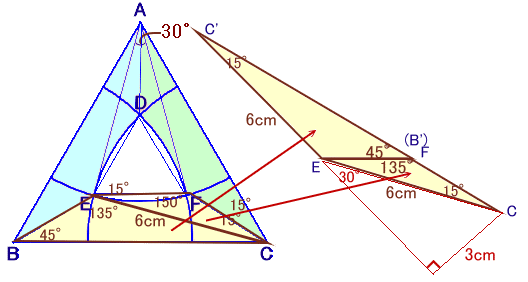
なお、EFの長さを求める方法として、次のようなものもあります。
解答例３の図より、EF＝FC＝EB＝ｂ。

BC＝AE・cos３０°＋EF＋FC・cos３０°
ａ＝ｂ×（√３＋１）

よって、ｂ＝ａ／（√３＋１）＝６√２／（√３＋１）
　　　　　　＝６√２（√３−１）／（√３×√３−１×１）
　　　　　　＝３（√６−√２）