第３４４問の解答

問題［平面図形］

問題図 左図のような一辺の長さが７cmの正八角形ＡＢＣＤＥＦＧＨがあります。

いま、辺ＡＢ上にＡＰ＝３cmとなる点Ｐを、辺ＨＡ上にＨＱ＝３cmとなる点Ｑをとりました。さらに、点Ｐおよび点Ｑと正八角形の各頂点を結びました。

このとき、図中の印のついた角度（ピンク色の部分）の和は何度でしょうか。

　

解答例１

長野　美光さん、ＩＣさん、小金井のチンジャラさん、あほあほまんさん、ふじさきたつみさん、土居　千珠さん、ステップ　ばい　ステップさん、2-5　ゆたさん、有無相生さん、他

参考図１

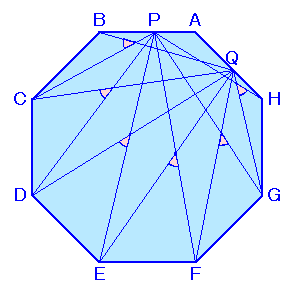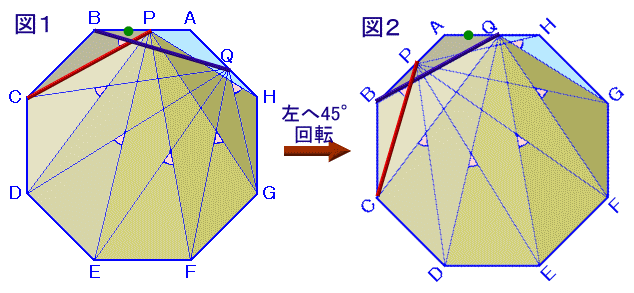
元の図形（図１）と、中心を軸に左へ４５度だけ回転した図２とを比較すると、
同じ色で塗りつぶした三角形どうしは合同であることが分かります。

すなわち、
　△PBC≡△QAB、△PCD≡△QBC、
　△PDE≡△QCD、△PEF≡△QDE、
　△PFG≡△QEF、△PGH≡△QFG。　・・・　（１）

よって、
　QBを４５度回転→PC、QCを４５度回転→PD、
　QDを４５度回転→PE、QEを４５度回転→PF、
　QFを４５度回転→PG、QGを４５度回転→PH
となります。

従って、
　QBとPCの交角＝QCとPDの交角
＝QDとPEの交角＝QEとPFの交角
＝QFとPGの交角＝QGとPHの交角＝４５度。

よって、これらの和＝４５度×６＝２７０度となります。

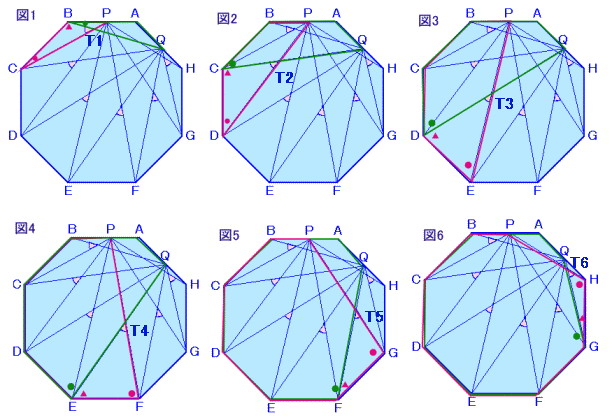
さて、（１）を詳しく言うと、まず△PBCと△QABについて、
　PB＝QA＝４cm、BC＝AB＝７cm、∠PBC＝∠QAB＝１３５°より、
二辺挟角が等しいので合同。
よって、PC＝QB。

次に、△PCDと△QBCについて、
　PC＝QB、CD＝BC＝７cm、∠PCD＝∠QBC＝１３５°より、
二辺挟角が等しいので合同。
よって、PC＝QB。

以下、同様にして（１）が成り立ちます。

答：　２７０度

以上

解答例２

ミヤーンさん、 他

参考図２

図１より、△PBC≡△QAB、
従って、∠BCP＋∠QBC＝∠ABQ＋∠QBC＝∠ABC＝１３５度。
よって、∠BT1C＝１８０度−（∠BCP＋∠QBC）＝１８０度−１３５度＝４５度。

図２より、四角形PBCD≡QABC、
従って、∠CDP＋∠QCD＝∠BCQ＋∠QCD＝∠BCD＝１３５度。
よって、∠CT2D＝１８０度−（∠CDP＋∠QCD）＝１８０度−１３５度＝４５度。

以下、同様にして６つの角度とも４５度となり、
これらの和は４５度×６＝２７０度となります。

（その他の解法）