第３４５問の解答

問題［場合の数］

左図のような、１階と２階をつなぐ５段の階段（５段目は２階）があります。

この階段を１階にいるマサルさんが、１段ずつ、１段とばしの片方または両方を使って１往復します。
このとき、どの階段も、上りまたは下りの少なくともいずれか一方で踏むものとします。

では、このような１往復の仕方は何通りあるでしょうか。

　

解答例１

辻。さん、まるケンさん、15KARATSOULさん、sugitakukunさん、トトロ＠Ｎさん、ハリスさん、たけちゃんさん、がんばるさやかですさん、takaisaさん、kasamaさん、あほあほまんさん、●●●●●●さん、小西孝一さん、有無相生さん、M.Hossieさん、ミミズクはくず耳さん、ねこやんさん、幽玄太郎さん、abcdeさん、BossFさん、ふじさきたつみさん、mindsさん、フランク長いさん、Drkさん、東洋の計算機さん、他


	１階から２階へ進むには、図１のように８パターンの場合があります。ただし、各段について、数字の１＝その段を踏む、0＝踏まないを表します。次に上りの各パターンで場合分けします。パターンＡ：既に全ての段を踏んでいるので、下りはどのパターンでもＯＫ・・・８通りパターンＢ：上りで踏んでいない４段目を踏むＡ、Ｃ、Ｄ、Ｆ、Ｈ　・・・　　　　５通りパターンＣ：上りで踏んでいない３段目を踏むＡ、Ｂ、Ｄ、Ｅ、Ｆ、Ｇ　・・・　　６通りパターンＤ：上りで踏んでいない２段目を踏むＡ、Ｂ、Ｃ、Ｆ、Ｇ、Ｈ　・・・　　６通りパターンＥ：上りで踏んでいない２、４段目を踏むＡ、Ｃ、Ｆ、Ｈ　　　・・・　　４通りパターンＦ：上りで踏んでいない１段目を踏むＡ、Ｂ、Ｃ、Ｄ、Ｅ　　　・・・　　５通りパターンＧ：上りで踏んでいない１、４段目を踏むＡ、Ｃ、Ｄ　　　　　・・・　　３通りパターンＨ：上りで踏んでいない１、３段目を踏むＡ、Ｂ、Ｄ、Ｅ　　　・・・　　４通り従って、　合計＝８＋５＋６＋６＋４＋５＋３＋４＝４１通りとなります。答：　４１通り以上

解答例２

ＩＣさん、CRYING DOLPHINさん、Toru Fukatsuさん、他


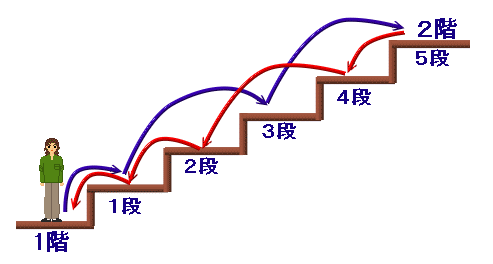
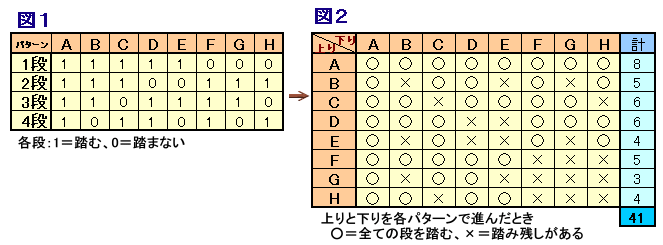
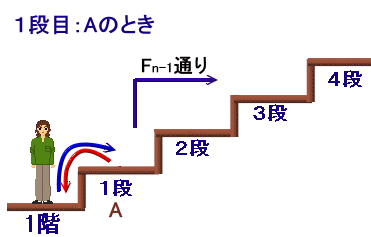
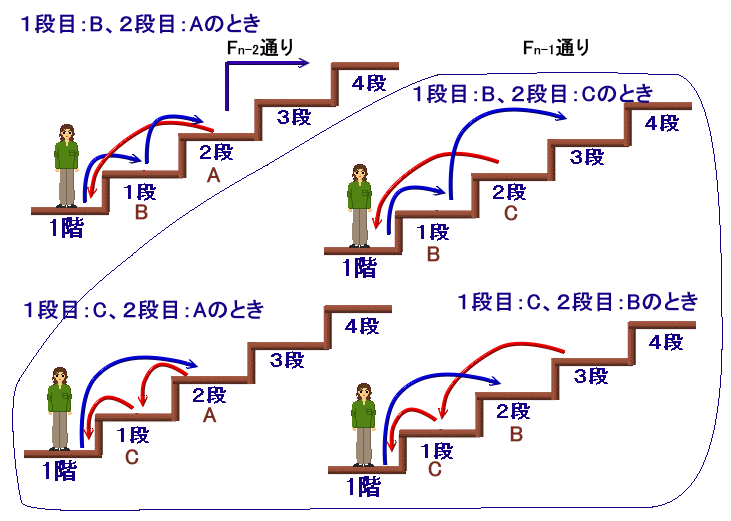
	２階までの段数がn段あるとして、場合の数をF_nとし、nに関する漸化式を考えます。まず、F₁＝１、F₂＝３は明らか。 n≧３のとき、第１段、第２段の踏み方によって場合分けします。ただし、以下では、A：上り・下りとも踏む、B：上りのみ踏む、C：下りのみ踏むと表します。（１）第１段を上り・下りとも踏むとき第１段を１階と見なせば、残り(n-1)段について上り・下りのいずれかでは踏んでいることからF_n-1通り（２）第１段を上りのみ、第２段は両方とも踏むとき第２段を１階と見なせば、残り(n-2)段について上り・下りのいずれかでは踏んでいることからF_n-2通り（３）第１段を上りのみ、第２段は下りのみ踏むとき（４）第１段を下りのみ、第２段は両方踏むとき（５）第１段を下りのみ、第２段は上りのみ踏むとき（３）では、上りで１階から２段目に上るのを、１段目から上ることに置き換えて、（４）、（５）では、上りで１階から２段目に上るのを、１段目から上ることに置き換えます。そして、それぞれ第１段を１階とみなせば、（４）は２段目を両方、（５）は上りのみ、（３）は下りのみ踏んでいるので、これらを合わせると、２段目およびそれ以降の合計(n-1)段について上り・下りのいずれかでは踏んでいることからF_n-1通り従って、（１）～（５）より、F_n＝２F_n-1＋F_n-2が成り立つことが分かります。よって、 n＝３のとき、F₃＝２F₂＋F₁＝２×３＋１＝７通り n＝４のとき、F₄＝２F₃＋F₂＝２×７＋３＝１７通り n＝５のとき、F₅＝２F₄＋F₃＝２×１７＋７＝４１通りとなり、本問では、F₅＝４１通りとなります。

（その他の解法）

プログラム（Jsva,Excelなど）で計算　・・・　ちばけいすけさん、???さん、他
　