第３４６問の解答

問題［平面図形］

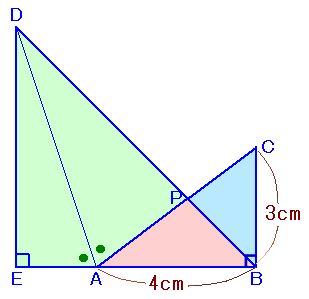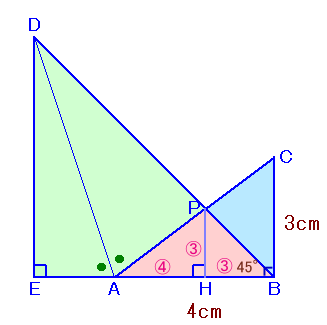
左図で、△ＡＢＣはＡＢ＝４cm、ＢＣ＝３cm、ＡＣ＝５cmの直角三角形、△ＥＢＤは、ＥＢ＝ＥＤの直角二等辺三角形です。

また、∠ＤＡＥ＝∠ＤＡＰとなっています。（ＰはＡＣとＤＢの交点）

このとき、△ＰＡＢの面積を求めてください。
　

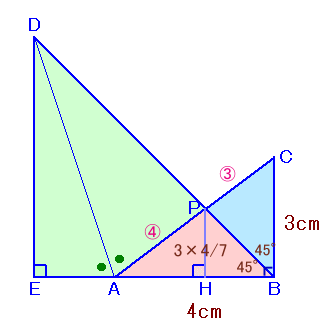
解答例１

ミヤーンさん、CRYING DOLPHINさん、ゆんななこさん、永井　暁さん、takaisaさん、M.Hossieさん、小西孝一さん、ミミズクはくず耳さん、ふじさきたつみさん、他


	点ＰからＡＢに下ろした垂線の足をＨとします。 △ＰＡＨと△ＣＡＢは相似だから、　ＡＨ：ＰＨ＝ＡＢ：ＣＢ＝４：３　・・・　（１）また、△ＰＨＢは△ＤＥＢと相似な直角二等辺三角形なので、　ＰＨ＝ＨＢ　・・・　（２）従って、（１）、（２）より、　ＰＨ＝ＡＢ×３/７＝４×３/７＝１２/７cm よって、　△ＰＡＢ＝１/２×ＡＢ×ＰＨ＝１/２×４×１２/７＝２４/７cm²。答：　２４/７cm² 以上

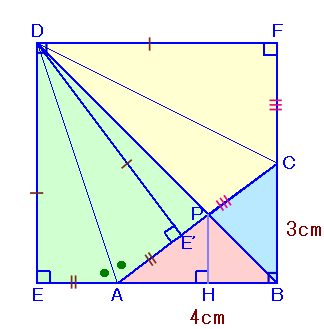
解答例２

ＪＵＮさん、たかし４さん、東洋の計算機さん、あほあほまんさん、他


	解答例１同様、Ｈを垂線の足とします。 △ＤＥＢは直角二等辺三角形より、∠ＤＢＥ＝４５°、従って、∠ＣＢＤ＝９０－４５＝４５°、よって、∠ＤＢＥ＝∠ＣＢＤ。すなわち、ＢＰは∠ＣＢＡの二等分線となることから、ＣＰ：ＰＡ＝ＢＣ：ＢＡ＝３：４よって、ＰＨ＝ＢＣ×４/（４＋３）＝３×４/７＝１２/７cm。以下同様。

（その他の解法）

ＤＥとＣＡの延長の交点をＦとして相似を用いて計算　・・・　ponta55555さん、他

ＡＨ＝ｘとおき、ｘに関する方程式を解く　・・・　ハラギャーテイさん、他

座標で考えＰのy座標に関する方程式を解く　・・・　有無相生さん、他

(参考)

中村明海さん、小金井のチンジャラさん、CRYING DOLPHINさん、他

今回の問題は、当初ＤＥの長さを求めるものとする予定だったそうです。
そこで、ＤＥを求めてみることにしましょう。

四角形ＤＥＢＦが正方形となるように点Ｆをとり、
ＤＡを軸として、△ＤＥＡを折り返したものを△ＤＥ'Ａとします。

∠DAE'＝∠ＤＡＥ＝∠DAPより、点E'は線分AP上にあることが分かります。

従って、△DE'A≡△DEAより、
　∠DE'A＝∠DEA＝９０°、およびE'A＝EA、DE'＝DE
となります。

さて、△DE'Cと△DFCを比べてみると、
　DCは共通、DE'＝DF、および∠DE'C＝∠DFC＝９０°より、
△DE'C≡△DFCとなることが分かります。

従って、
　DE×２
＝EB＋FB
＝（EA＋AB）＋（FC＋CB）
＝（E'A＋E'C）＋AB＋CB
＝AC＋AB＋CB
＝４＋３＋５
＝１２

よって、DE＝１２÷２＝６cmとなります。


	今回の問題は、当初ＤＥの長さを求めるものとする予定だったそうです。そこで、ＤＥを求めてみることにしましょう。四角形ＤＥＢＦが正方形となるように点Ｆをとり、ＤＡを軸として、△ＤＥＡを折り返したものを△ＤＥ'Ａとします。 ∠DAE'＝∠ＤＡＥ＝∠DAPより、点E'は線分AP上にあることが分かります。従って、△DE'A≡△DEAより、　∠DE'A＝∠DEA＝９０°、およびE'A＝EA、DE'＝DE となります。さて、△DE'Cと△DFCを比べてみると、　DCは共通、DE'＝DF、および∠DE'C＝∠DFC＝９０°より、 △DE'C≡△DFCとなることが分かります。従って、　DE×２＝EB＋FB ＝（EA＋AB）＋（FC＋CB）＝（E'A＋E'C）＋AB＋CB ＝AC＋AB＋CB ＝４＋３＋５＝１２よって、DE＝１２÷２＝６cmとなります。