第３４７問の解答

問題［平面図形］

問題図

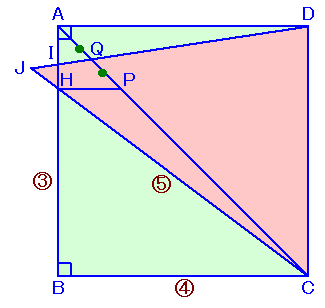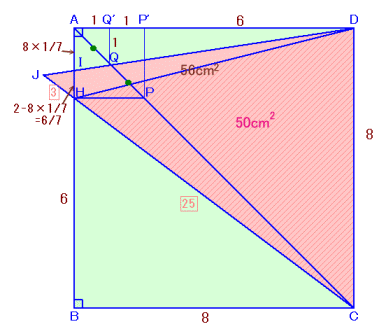
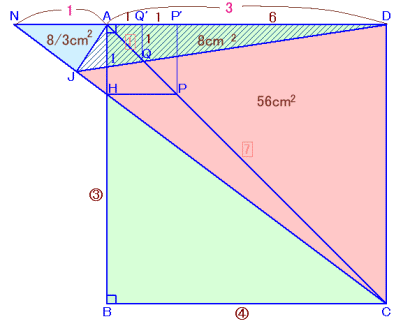
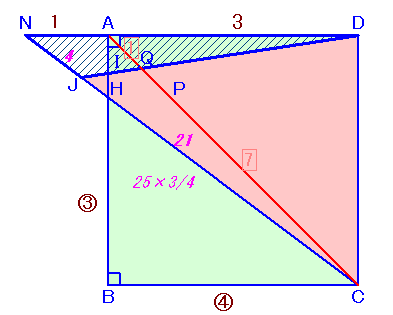
左図のような正方形ＡＢＣＤがあります。

いま、対角線ＡＣ上に点Ｐをとり、ＰＨとＢＣが平行になるように点Ｈを辺ＡＢ上にとったところ、ＨＢ：ＢＣ：ＣＨ＝３：４：５となったそうです。

次に、頂点ＤとＡＰの中点Qを通る直線と、直線ＣＨの交点をＪとして△ＤＪＣを作りました。すると、△ＤＪＣの面積は５６cm2となりました。

このとき、この正方形の面積を求めてください。
　

解答例１

ねこやんさん、午年のうりぼうさん、徳島算数小僧さん、筑紫丘高校新１年生さん、ふじさきたつみさん、ステップ　ばい　ステップさん、あほあほまんさん、大岡　敏幸さん、Banyanyanさん、M.Hossieさん、 他

点ＰおよびQからＡDに下ろした垂線の足をP'、Q'とし、
正方形の１辺の長さを８とします。

参考図１

題意より、
　HB＝P'D＝８×３/４＝６、
　AH＝AP'＝AB−HB＝２、
　AQ'＝Q'P'＝Q'Q＝AP'×１２＝１

△AIDと△Q'QDは相似より、AI＝AD×Q'Q/Q'D＝８×１/７＝８/７。

よって、　IH＝AH−AI＝２−８/７＝６/７。

従って、　IH：BC＝６/７：８＝３：２８。

△IJHと△DJHは相似より、JH：JC＝IH：BC＝３：２８。

よって、 △DHC＝△DJC×２５/２８＝５６×２５/２８＝５０cm2。

従って、 正方形ABCD＝△DHC×２＝１００cm2。
　

答：　１００cm2

以上

解答例２

まるケンさん、 他

CJとDAをそれぞれ延長して交わる点をNとします。

参考図２

解答例１と同様にして、AQ'：Q'D＝１：７。

△AQQ'と△ACDは相似より、AQ：QC＝AQ'：Q'D＝１：７。

従って、　△AQD：△CQD＝△AJQ：△CJQ＝１：７、
よって、　△AJD：△CJD＝１：７となり、
　△AJD＝△CJD×１/７＝８cm2。

また、ND：CD＝４：３で、AD＝CDより、NA：AD＝１：３、
従って、△NJA＝△AJD×１/３＝８/３cm2。

以上から、
　△NCD＝△NJA＋△AJD＋△CJD＝８/３＋８＋５６＝２００/３cm2、
　△ACD＝△NCD×３/４＝２００/３×３/４＝５０cm2。

よって、正方形ABCD＝△ACD×２＝１００cm2。
　

解答例３

高田修成さん、 他

解答例２同様、NをCJとDAの交点とします。

参考図３

解答例２と同様にして、AQ：QC＝１：７、NA：AD＝１：３。

△NJDと直線ACに関してメネラウスの定理より、
　NJ/JC×CQ/QA×AD/DN＝１、
　NJ/JC×７/１×３/４＝１。

よって、　NJ：JC＝４：２１。

△NHAと△NCDは相似より、NH：HC＝NA：AD＝１：３。

よって、NC＝２５とすると、
　HC＝NC×３/４＝７５/４、JH＝２１−７５/４＝９/４、
従って、JH：HC＝９/４：７５/４＝３：２５。

以下、同様。

（その他の解法）