第３４９問の解答

問題［場合の数］

【元の問題】

算チャレ小学校も新学期が始まりました。

マサル先生のクラスは、２０人学級です。始業式の日、マサル先生が「友だちは何人いますか？」という質問を生徒にしたところ、全員が「３人！」と答えたそうです。

そこで、マサル先生が生徒のトモエさんに、「じゃあお友だちを１人紹介してください。」と言うと、トモエさんはツヨシ君を紹介しました。マサルさんがツヨシ君に「じゃあトモエさん以外のお友だちを１人紹介してください。」と言うと、マサヒコ君を紹介しました。これをずっと続けたところ、最後にトモエさんが紹介されて、全員が１回ずつ紹介されたことになったということです。

では、このクラスで同じようにトモエさんから順に友だちを紹介していって、全員が１回ずつ紹介されて最後にトモエさんにかえってくるような「紹介順」は何通りあるでしょうか。ただし、ある紹介順と完全に逆順になっているものも、それぞれ１通りと数えるものとします。

【解答例で考えた問題】

友達関係をグラフで表し、生徒を点、友人関係を点と点を結ぶ辺で考えることにします。
友達関係が、正１２面体となっている場合について、紹介順の個数を求めて下さい。

解答例

マサルさん、nobuさん、中村明海さん、トトロ＠Ｎさん、むらかみさん、Taroさん、たかまつ　ろろさん、高橋　道広さん、まるケンさん、Miki Sugimotoさん、ずぱいさん、 他

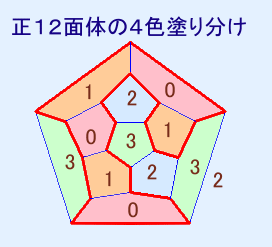
生徒の友人関係を図（グラフ）で表したときに、生徒を「点」、友人関係を点と点を結ぶ「辺」で表すことができます。
本問では、「点の数が２０、各点から出ていく辺の数は全て３」という条件を満たすグラフを考えることになります。
このとき、「紹介順」は、「全ての点を一度ずつ通るように辺をたどり元の点に戻る」という、いわゆるハミルトン閉路（向き有り）の数を求めることに帰着されます。

ところが、グラフのパターンによってハミルトン閉路の数は異なるので、一定の個数になるわけではありません。
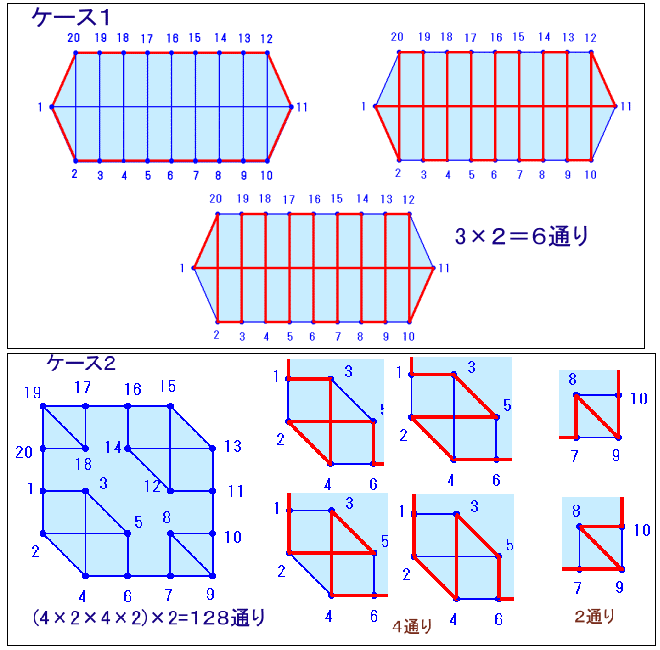
例えば、下図のケース１では６通り、ケース２では１２８通りになります。

まるケンさんがプログラムで全てのケースについて求めてみると、６から８４までの偶数全部と、８８、９６、１１２、１２８の個数になるパターンがあるようです。

参考図１

今回の問題について、出題者の意図は、「友達関係のグラフが正１２面体となるケース」を想定していたようです。
従って、以下では、正１２面体のケースに限って考えることにしましょう。
また、閉路の向きはとりあえず無視することにして、あとから２倍することにしましょう。

「正１２面体の頂点の数は２０個、各頂点から出ていく辺の数は全て３」だから、確かに題意を満たすグラフになります。

参考図２

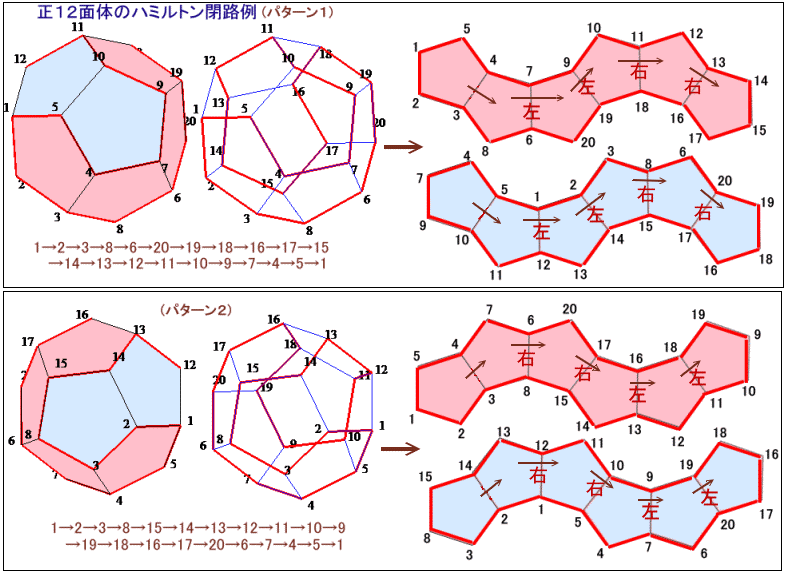
上記、２つのパターンは正１２面体のハミルトン閉路になっていますが、実は本質的な（回転移動などを除く）パターンは、この２通りしかないことが知られています。

以下では、この事実について考えてみましょう。

参考図３

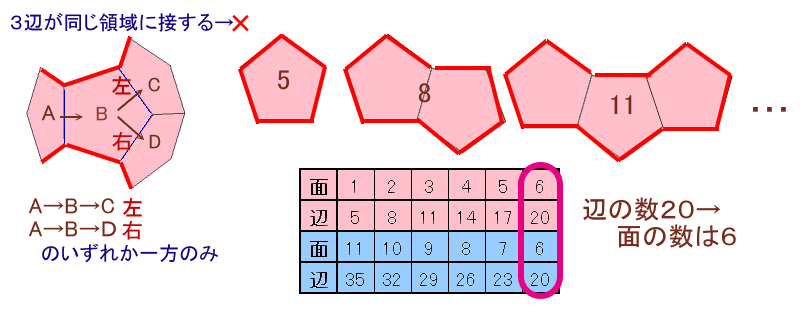
ハミルトン閉路によって、正１２面体の表面は２つの領域に分割されます。
一つの領域に属する面（正５角形）は、同じ領域に属する他の面と３個以上接することはありませんので、帯状をしていることになります。

また、領域に含まれる面の個数によって、周囲にある辺の個数は上記のように一意的に求まります。
ところが、ハミルトン閉路となるには、辺の個数＝頂点の個数＝２０個となる必要がありますので、面の個数はそれぞれ６個ずつに分割されることになります。

さて、６個の面からなる帯状の領域で、どのようなパターンになるかを、次のように考えてみます。
すなわち、端の面から次の面へ進んだあと、それ以降の面へは、左へ進むか右に進むの２通りしかありません。
従って、最大２4＝１６通りとなりますが、左と右を置き換えることにより、左≧右の場合だけ考えることにします。

参考図４
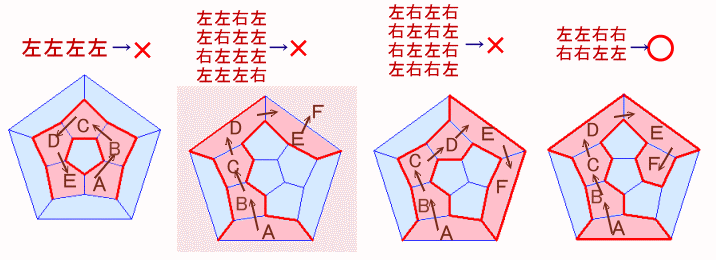
（正１２面体を平面に展開した図。外側も１個の面になっている。）

  • 左が４個続く場合　・・・　元の面に接することになり不可

  • 左が３個の場合　・・・　いずれも元の面と接することになり不可

  • 左＝右＝２個の場合　・・・　左と右がそれぞれ連続するケースのみＯＫ

従って、左左右右または右右左左の２ケースのみということが分かります。

では、以上の事実にもとづいて、いよいよハミルトン経路数を求めてみましょう。

参考図５

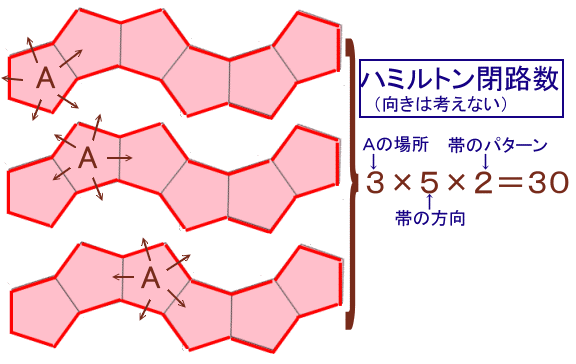
正１２面体のある面（Ａとします）を固定して考えます。

Ａを含む領域について、Ａが端から数えて何番目の位置にあるかは、６÷２＝３通りとなります。
また、Ａから進む帯の方向はＡの辺の数＝５通りあり、さらに帯のパターンは上記２通りなので、
　合計＝３×５×２＝３０通り
と分かります。

最後に、閉路の向きを考えて、３０×２＝６０通りと求まります。

答：　６０通り

以上

（参考）

「正多面体を解く」（一松信著：東海大学出版会）によれば、ある頂点からハミルトン閉路の辺に沿って進むパターンは、頂点に来るごとに左右どちらかに進むかで考えると、
　左左左左右右右右左右左右（これを２回反復）または右右右右左左左左右左右左（これを２回反復）
のいずれかになるようです。

残念ながら、この証明が記載されてなく、少し考えても思いつきませんでしたので、上記解法を考えてみました。

なお、ハミルトン閉路と正１２面体の４色塗り分けとは関連しています。
下図のように、ハミルトン閉路で分割された２つの領域を、それぞれ２色を使って交互に塗り分けていくと表面全体は４色で塗り分けられています。
逆に、４色で塗り分けられたときに、そのうちの２色ずつをとった２つの領域は、それぞれ閉じられた領域になっていて、分割の境界線がちょうどハミルトン閉路になっています。

参考図６

（その他の解法）