第３５０問の解答

問題［空間図形］

問題図

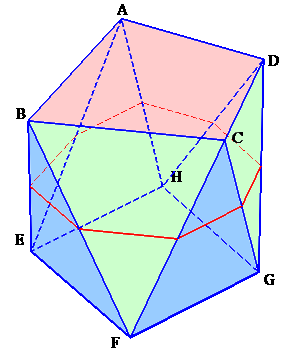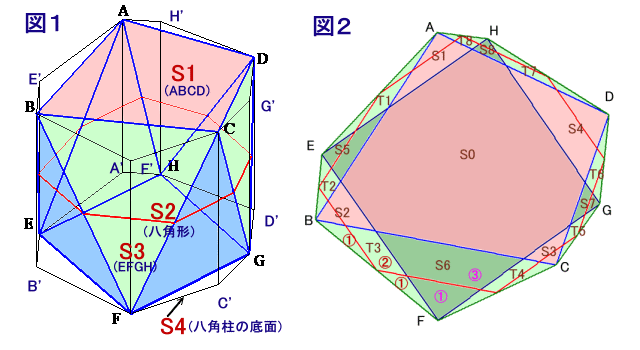
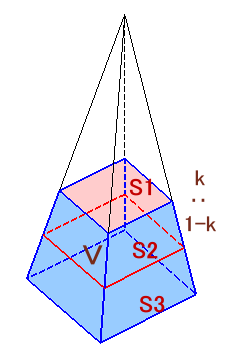
左図のような、四角形２枚（面ＡＢＣＤと面ＥＦＧＨ）と三角形８枚でできた１０面体ＡＢＣＤ−ＥＦＧＨがあり、面ＡＢＣＤと面ＥＦＧＨは平行になっています。

また、面ＡＢＣＤと面ＥＦＧＨの面積はともに２０cm2、この１０面体の高さ（面ＡＢＣＤと面ＥＦＧＨの距離）は６cmです。

ここで、この１０面体をちょうど高さが半分になるように切断したところ（図の赤い線）、切断面の面積が２２cm2となったそうです。

このとき、この１０面体の体積を求めてください。

解答例１

M.Hossieさん、フランク長いさん、takaisaさん、ponta55555さん、 他


A、B、C、Dから底面に下ろした垂線の足をA'、B'、C'、D'、および、E、F、G、Hから上面に下ろした垂線の足をE'、F'、G'、H'とします。また、図２は真上から立体を見た図です。

参考図１

図１より、十面体は、上面をAE'BF'CG'DH'、底面をA'EB'FC'GD'Hとする八角柱から、８個の三角錐を除いたものとなります。

従って、求める十面体の体積をVとすると、
　V＝八角柱−（三角錐A-A'HE＋三角錐B-B'EF＋三角錐C-C'FG＋三角錐D-D'GH）
　　　　　　　−（三角錐E-E'AB＋三角錐F-F'BC＋三角錐G-G'CD＋三角錐H-H'DA）　・・・　（１）

上面の面積をS１、真ん中の八角形の面積をS２、底面の面積をS３、八角柱の上面・底面の面積をS４とし、
図２で分割された各三角形の面積を、T1、・・・、T８、s1、・・・、s8とします。

すると、題意より、例えばT３は、赤い線の内側と外側に２等分、Ｓ６は３：１に分割されることから、
S４−S２＝（T1＋T2＋T3＋T4＋T5＋T6＋T7＋T8）/２
　　　　　　　＋（s1＋s2＋s3＋s4）/４＋（s5＋s6＋s7＋s8）/４　・・・　（２）
S２−S１＝（T1＋T2＋T3＋T4＋T5＋T6＋T7＋T8）/２
　　　　　　　＋（s5＋s6＋s7＋s8）×３/４−（s1＋s2＋s3＋s4）/４　・・・　（３）
S２−S３＝（T1＋T2＋T3＋T4＋T5＋T6＋T7＋T8）/２
　　　　　　　＋（s1＋s2＋s3＋s4）×３/４−（s5＋s6＋s7＋s8）/４　・・・　（４）

Ｔ＝T1＋T2＋T3＋T4＋T5＋T6＋T7＋T8、s＝s1＋s2＋s3＋s4、s'＝s5＋s6＋s7＋s8とおくと、

｛（３）＋（４）｝÷２より、
　　S２−（S１＋S３）/２
　＝（T/２＋s'×３/４−s/４）＋（T/２＋s×３/４−s'/４）
　＝T/２＋s/４−s'/４
　＝S４−S２
となります。

よって、
　　S４＝S２×２−（S１＋S３）/２　・・・　（５）
　　　　＝２２×２−（２０＋２０）/２
　　　　＝２４cm2
となります。

さて、立体の高さをh＝６cmとおくと、
　三角錐A-A'HE＝１/３×△A'HE×h、三角錐B-B'EF＝１/３×△B'EF×h
　三角錐C-C'FG＝１/３×△C'FG×h、三角錐D-D'GH＝１/３×△D'GH×h
より、
　三角錐A-A'HE＋三角錐B-B'EF＋三角錐C-C'FG＋三角錐D-D'GH
＝１/３×（△A'HE＋△B'EF＋△C'FG＋△D'GH）×h
＝１/３×（S４−S３）×h　・・・　（６）

同様に、
　三角錐E-E'AB＋三角錐F-F'BC＋三角錐G-G'CD＋三角錐H-H'DA
＝１/３×（△E'AB＋△F'BC＋△G'CD＋△H'DA）×h
＝１/３×（S４−S１）×h　・・・　（７）

よって、（１）、（６）、（７）より、
　V＝S４×h−１/３×（S４−S３）×h−１/３×（S４−S１）×h
　　＝１/３×（S４＋S１＋S３）×h
　　＝１/３×[｛S２×２−（S１＋S３）/２}＋S１＋S３]×h
　　＝１/６×（S１＋S２×４＋S３）×h　・・・　（８）
　　＝１/６×｛２０＋２２×４＋２０｝×６
　　＝１２８cm2
と求まります。

答：　１２８cm3

以上

解答例２

中村明海さん、 他

解答例１の（８）は、定積分に関するシンプソンの公式になっています。

シンプソンの公式は、a、b、cが等間隔に並ぶとき、
　２次関数 f(x)を区間[a、c]で積分すると、 (c-a)(f(a)+4f(b)+f(c))/６というものです。

解答例１と同様に、十面体を八角柱から８個の三角錐を除いたものと考えると、
八角柱、各三角錐とも水平に切った断面の面積は、底面からの高さに関する２次関数として表されるので、
これらの合計である十面体についても断面積は高さに関する２次関数となり、シンプソンの公式が成り立ちます。

参考図２

例えば、上図は四角錐（高さh）を頂点からk：(1-k)で切断した立体 の場合、
　V＝１/３×S３×h×（1−k3）
となります。
一方、
　V'＝（１−k）×h×｛S１＋S２×４＋S３｝/６
　　＝（１−k）×h×[S３×（１−k2）＋S３×｛（1＋k）/２｝2＋S３]/６
　　＝h×S３×（１−k）×（１＋k＋k2）/３
　　＝h×S３×（1−k3）/３
　より、確かにV'＝Vとなり、シンプソンの公式が成り立っています。

従って、
　十面体の体積＝（２０＋２２×４＋２０）/６×６＝１２８cm2
と求まります。

（その他の解法）