第３５１問の解答

問題［推理］

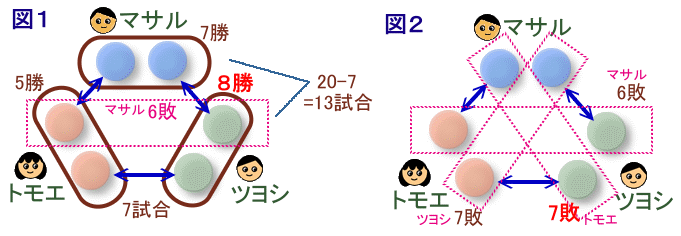
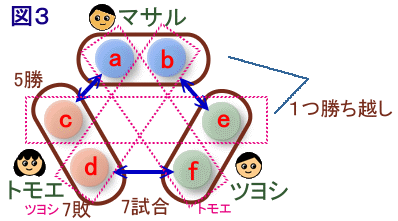
マサルさん、トモエさん、ツヨシ君の３人がチェスの試合を朝から夕方まで行っています。

ちょうど２０試合が終わったところで対戦成績表を見ると、マサルさんは１つ勝ち越し、トモエさんの勝ち数は５、ツヨシ君の負け数は７で、トモエさんとツヨシ君は７回対戦していたということです。（引き分けはありません）

このとき、次の各問いに答えてください。
　（１）　トモエさんは何敗しているでしょうか。
　（２）　ツヨシ君は何勝しているでしょうか。

Hamayanさん、まるケンさん、高田修成さん、小西孝一さん、dottoreさん、有無相生さん、あさみかずみさん、フランク長いさん、M.Hossieさん、kasamaさん、クララさん、鳳仙花さん、大岡　敏幸さん、他


	図１のように、各対戦を矢印で表して、自分側に勝ち数（負け数＝相手側の勝ち数）を表すことにします。図１で分かるように、マサルさんが試合に出なかったのは、トモエさんとツヨシ君が対戦した７試合のみです。従って、マサルさんの試合数＝２０－７＝１３試合と分かります。マサルさんは、勝ち数が負け数より１つ多いので、７勝６敗となります。各人の勝ち数合計＝各人の負け数合計＝試合数合計＝２０試合だから、ツヨシ君の勝ち数＝２０－（マサルさんの勝ち数＋トモエさんの勝ち数）＝２０－（７＋５）＝８勝トモエさんの負け数＝２０－（マサルさんの負け数＋ツヨシ君の負け数）＝２０－（６＋７）＝７敗と求まります。答：　トモエ：７敗、ツヨシ：８勝以上

DrKさん、ハラギャーテイさん、他


	解答例１と同様の図３で表し、各対戦ごとの勝ち数を未知数とする方程式を考えます。図３より、 (a＋b)－(c＋e)＝１　・・・　（１） c＋d＝５　・・・　（２） b＋d＝７　・・・　（３） d＋f＝７　・・・　（４） a＋b＋c＋d＋e＋f＝２０　・・・　（５）となります。（２）、（３）、（４）より、 c＝５－d、　b＝７－d、　f＝７－d　となるので、これらを（１）、（５）に代入すると｛a＋(７－d)｝－｛(５－d)＋e｝＝１ a－e＝－１　・・・　（１）’ a＋(７－d)＋(５－d)＋d＋e＋(７－d)＝２０ a＋e＝１＋２d　・・・　（５）’ （１）’、（５）’、より、 a＝d、　e＝d＋１を得ます。従って、トモエさんの負け数＝a＋f＝d＋(７－d)＝７敗ツヨシ君の勝ち数＝e＋f＝(d＋１)＋(７－d)＝８勝となり、dの値にかかわらず一意的に求まることが分かります。

トモエｖｓツヨシを　５－２と決めつけて　・・・　長野　美光さん他
　

ＥＸＣＥＬで求める　・・・　Taroさん、他
　