第353問の解答
問題[場合の数]
|
|
|
|
|
|
|
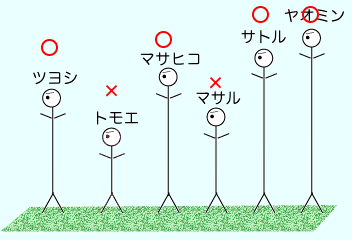 |
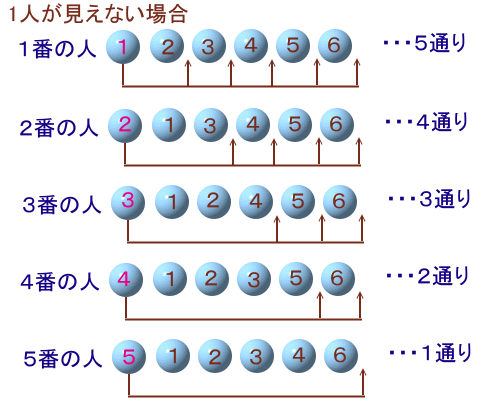
トモエさん、マサルさん、ツヨシ君、マサヒコ君、サトルさん、ヤオミン君の6人の身長はそれぞれ120cm、140cm、160cm、180cm、200cm、220cmです。 この6人が縦に1列に並ぶとき、背の低い順に並べば全員が前方を見ることが出来ますが、 左図のような並び方をすると、ツヨシ君、マサヒコ君、サトルさん、ヤオミン君の4人は前方を見ることができますが、トモエさん、マサルさんは前の人の背中しか見えません。 では、この6人の並び方で、「4人だけが前方を見ることができる」ような並び方は何通りあるでしょうか。 |
|
|
|
|
|
|
解答例1
まるケンさん、takaisaさん、ponta55555さん、中村明海さん、 他
|
|
|
|
|
|
|
|
|
|
|
|
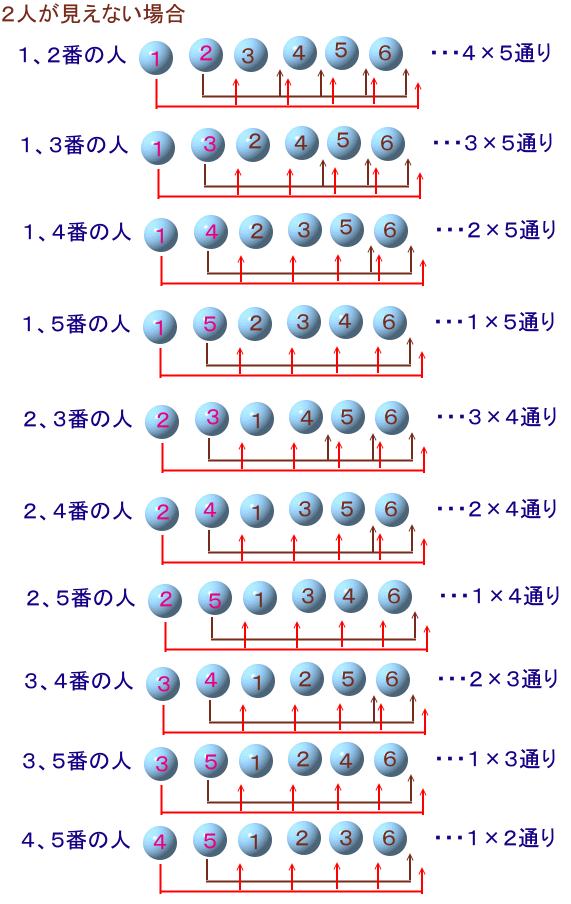
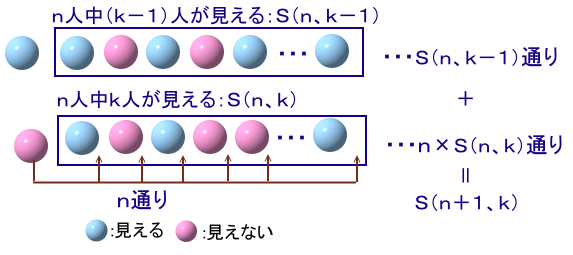
解答例2
Toru Fukatsuさん、清川 育男さん、ミミズクはくず耳さん、 他
|
|
|
|
|
|
|
|
|
|
|
|
(その他の解法)
プログラムで計算 ・・・ 高田修成さん 、Miki Sugimotoさん、kasamaさん、ハラギャーテイさん、 ???さん、他
1番高い人の位置を決めて場合分けし、数え上げる・・・ 遠い山のぽきょぽんさん、トトロ@Nさん、ポケモンハルカさん、M.Hossieさん、ふじさきたつみさん、シイサンさん、拓パパさん、他
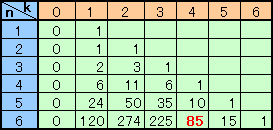
人数が少ないときをまず数えて、これを利用して場合分けし、数え上げる・・・ 有無相生さん、他