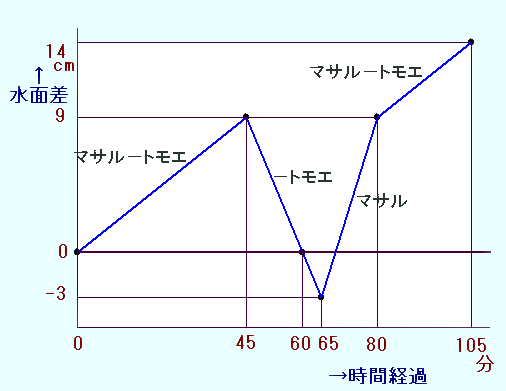
第３５４問の解答
問題［速さの問題］
マサルさんとトモエさんがそれぞれの直方体の容器（最初は空）にポンプで井戸水をくむことにしました。 まず２人は１２時ちょうどに同時に井戸水をくみ始めました。
すると１２時４５分には２人の容器の水面の高さの差は９cmになっており、これを見たマサルさんはしばらく休むことにしました。すると１時ちょうどに２人の容器の水面の高さは同じになりました。
その後１時５分にマサルさんが再び水をくみ始め、トモエさんは休むことにしました。
マサルさんの容器とトモエさんの容器の水面の高さの差が再び９cmになったところで再びトモエさんが水をくみはじめ、マサルさんの容器がいっぱいになったところで２人同時に作業を中止したそうです。
このとき、マサルさんの容器とトモエさんの容器の水面の高さの差は１４cmでした。では、マサルさんの容器の高さを求めてください。
解答例１
世羅君さん、ヒデー王子さん、拓パパさん、kasamaさん、Nakariさん、岩木伸二さん、小西孝一さん、M.Hossieさん、中村明海さん、ふじさきたつみさん、 DrKさん、トトロ＠Ｎさん、kumaさん、クララさん、takaisaさん、辻。さん、あさみかずみさん、大岡 敏幸さん、ななしぞうさん、他
ダイアグラムを参考にして考えます。
縦軸を、マサルさんの容器とトモエさんの容器の水面差、横軸を経過時間にします。
最初の４５分間で水面差が９cmになることから、５分間で１cmずつ差がつくことになります。
次の１５分間で９cmの差がなくなったということは、トモエさんの汲む速さは５分間で３cm。
よって、次の５分間では、マサルさんのほうが３cm低くなります。また、マサルさんの汲む速さは、５分間で３＋１＝４cmと分かります。
従って、再び水面差が９cmになるには、９−（−３）＝１２cmだけマサルさんは汲むことに
なるので、所要時間は１２cm/5分÷４cm＝１５分。最後に水面差が１４ｃｍになるのは、（１４cm−９cm）÷１cm/5分＝２５分。
以上から、マサルさんが水を汲んでいる時間は、
０〜４５分までの４５分間と６５分〜１０５分の４０分間、
合計８５分間と求まります。従って、この間に水面の高さは、４cm/5分×８５分＝４×１７＝６８ｃｍ増えることになります。
よって、容器の高さは６８cmとなります。
答： ６８cm
以上
