第３５６問の解答
問題［空間図形］
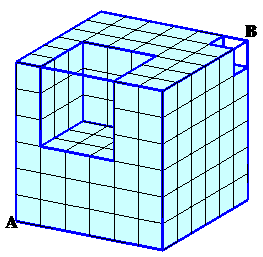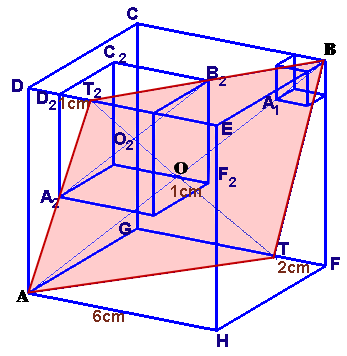
左図のように、１辺が１cmの小立方体を積み上げて、一辺の長さが６cmの立方体を作りました。次に、この立方体から計２８個の小立方体を取り除きました。
この立体を、Ａ点およびＢ点を通るような平面で切断して、体積がちょうど２等分されるようにします。
このとき、小立方体は何個切断されるでしょうか。
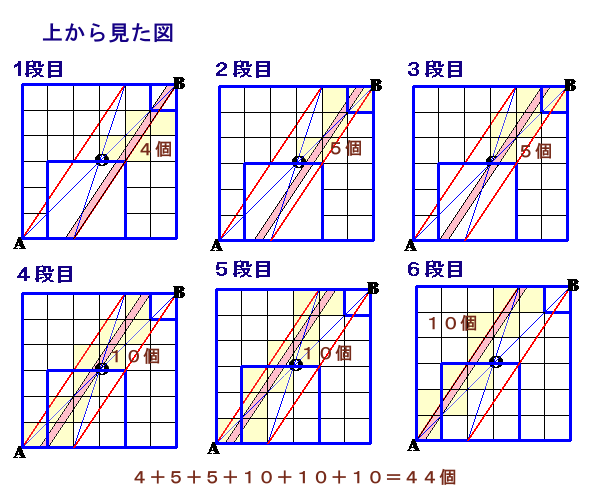
解答例１
トトロ＠Ｎさん、圭太さん、かぱさん、CRYING DOLPHINさん、遠い山のぽきょぽんさん、takaisaさん、中村明海さん、JUNさん、小西孝一さん、ミミズクはくず耳さん、kasamaさん、高橋 道広さん、 他
（補題）点対称の空間図形の中心を通る平面は、この図形を２等分する。
逆に、この図形を２等分する平面は中心を通る。
(証明)
前半は明らか。
後半は次のように背理法で考えましょう。
すなわち、ある平面２が、この図形を２等分し、かつ図形の中心Ｏを通らないとします。ここで、平面２に平行で中心Ｏを通る平面を平面１とします。
すると、平面１は補題の前半より図形を２等分することになりますが、これは仮定と矛盾します。よって、補題の後半部分も成り立つことが分かります。
問題の平面（Pとします）は対角線ＡＢを含むので、最初の立方体（C０とします）の中心Ｏを通ります。
また、対角線ＡＢは右上の小立方体の対角線ＢＡ１を含むので、Pはこの中心も通ることになり、
小立方体も２等分します。従って、題意よりPは３×３×３cmの立方体（C２とします）も２等分することになり、
従って補題後半より立方体C２の中心Ｏ2も通ります。ところで、ＯはC２の底面に含まれる辺上の点で、頂点Ｆ2から1cmの距離にあります。
よって、Ｏ2に関してＯと対称な点T2も平面Pに含まれます。T2は、C2の頂点D2から1cm、従ってC0の頂点Dから2cmの距離にあります。
よって、Oに関してからT2と対称な点Tも平面Pに含まれます。
以上から、平面Pは平行四辺形BT2ATを含むことになるので、立方体C０を上から1cmごとに区切って考えると下図のようになります。
従って、平面Pが切断する小立方体の個数は、
上の段から、４、５、５、１０、１０、１０個、
よって、合計４４個を切断することが分かります。答： ４４個
以上
（その他の解法）
- 座標系で考える ・・・ M.Hossieさん、DrKさん、他
