第３５７問の解答

問題［ 平面図形］

問題図

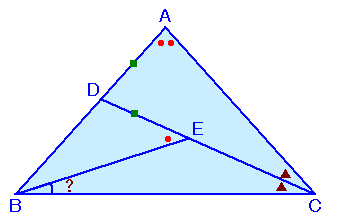左図のようなＡＢ＝ＡＣの二等辺三角形ＡＢＣがあります。

いま、∠Ｃの二等分線と辺ＡＢの交点をＤとします。そして、ＣＤ上にＡＤ＝ＤＥとなるような点Ｅをとり、頂点Ｂと結んだところ、∠ＤＥＢの大きさが∠Ａの大きさのちょうど半分になったそうです。

このとき、∠ＥＢＣは何度になるでしょうか？

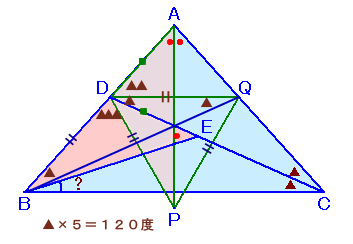
解答例１

nobuさん、kataさん、 他

点Dを中心に△DBEを回転して点Eが点Aと重なるようにし、点Bが点Pに移動するものとします。
また、Dを通ってBCに平行に引いた直線とACの交点をQとします。

参考図１

∠DAP＝∠DEB＝∠BAC÷２より、APとDQは直交することが分かります。
よって、△PDQはPD＝PQの二等辺三角形となります。

DQとACが平行より、∠DQB＝∠QDC＝∠DCB、および　∠DBQ＝∠ACD＝∠DCB。

従って、△DBQはDB＝DQの二等辺三角形となります。
よって、△PDQは正三角形となることが分かります。

さて、∠EDB＝∠ADPより、∠PDB＝∠ADC＝∠DCB×３。
よって、∠ADQ＋∠PDB＝∠DCB×５＝１８０−６０＝１２０度。

従って、∠DCB＝１２０÷５＝２４度と分かります。
すると、∠DEB＝∠CAP＝９０−２４×２＝４２度。

よって、∠EBD＝∠DEB−∠DCB＝４２−２４＝１８度と求まります。

答：　１８度

以上

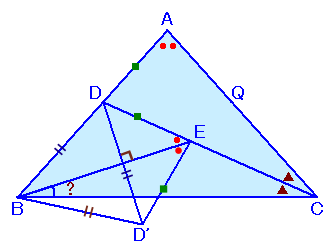
解答例２

マサルさん、 他

BEを軸として点Dを折り返した点をD'とします。

参考図２

すると、△BD'DはBD＝BD'の二等辺三角形、△EDD'はED＝ED'の二等辺三角形となります。

従って、∠D'EB＝∠DEBより、∠D'ED＝∠DEB×２＝∠CAB。
よって、△EDD'は△ABCと相似となります。

従って、ED'：DD'＝AC：BC　・・・　（１）

ところで、CDは△ABCに関して、∠ACBの二等分線なので
　AD：DB＝AC：BC　・・・　（２）

（１）、（２）より、
　ED'：DD'＝AD：DB

従って、AD＝ED＝ED'より、DD'＝DB。
よって、△BD'Dは正三角形と分かります。

従って、∠DBE＝∠DBD'÷２＝６０度÷２＝３０度。

ここで、ｘ＝∠DCB、ｙ＝∠CAB÷２とおくと、
２ｘ＋ｙ＝９０　・・・（１）
１８０−（ｘ＋２ｙ）＋２ｘ＝１２０より、−ｘ＋２ｙ＝６０　・・・　（２）

（１）、（２）より、ｘ＝２４度、ｙ＝４２度を得ます。

よって、∠EBC＝ｙ−ｘ＝１８度と求まります。

（その他の解法）