第３５９問の解答

問題［場合の数］

問題図

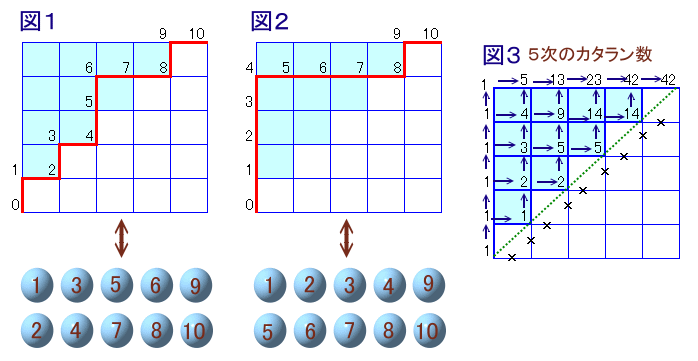
左図のような座席数１０席（立ち見専用）の会場で、マサルさんのコンサートが行われることになりました。

マサルはステージ上を動き回るので、立ち見席にいるファン達は（マサルの動きにあわせて）北または西方向を向いて鑑賞します。

では、１０人とも背の高さが異なっていたとき、全員が、前の人に視界をさえぎられることなくコンサートを鑑賞することができるような席の割り当て方は何通りあるでしょうか。

解答例１

takaisaさん、萬田銀次郎さん、小西孝一さん、M.Hossieさん、まるケンさん、Taroさん、 他

本問の積の割り当て方（A)と５×５のマス目上の進み方（B)とを比較してみます。

参考図１

１０人のファンについて、背の低い順に１〜１０まで番号を振ります。

すると、（A)は、次のような規則（C)で座席を決めることに対応することが分かります。

  • １番の人から１０番の人まで順番に、前列（北側）に座るか、後列（南側）に座るかを決めてもらいます。

  • ただし、前列と後列に座った人の数が一致するときは前列しか選べません。

  • そして、その列の右端に座ることにします。

また、上図の図１、図２のように、（C)と（B)は、

  • 前列に座る⇔マス目の上（北）へ進む

  • 後列に座る⇔マス目の右（東）へ進む

  • 進む道は対角線上より左上に限る

のように１：１に対応させることができます。

従って、図３のように、マス目の左下から順番に上または右に進む場合の数を記入していくと、
右上では４２通りになることが分かります。

なお、このようなマス目の進み方の数は、カタラン数と呼ばれる数と一致することが知られています。
一般に、n次のカタラン数Kn＝2nCn/(n+1)で求まります。

従って、本問では５次のカタラン数となるので、
　K5＝10C5/６＝２５２/６＝４２通り
と分かります。

答：　４２通り

以上

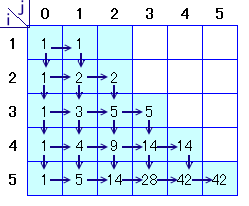
解答例２

中村明海さん、高橋　道広さん、 他

漸化式で考えます。小さい人から順序良く （i+j）人目までを並ばせたとき、
前列に i 人、後列に j 人となる場合の数を a(i,j)通りとします。

題意より、

  • a(i,j) = 1 (j=0)

  • a(i,j) = 0 (j>i)

  • a(i,j) = a(i-1,j)+a(i,j-1)

が成り立ちますので、下表のように順次計算して求めることができます。

参考図２

よって、４２通りと分かります。

（その他の解法）