第３６０問の解答

問題［空間図形］

問題図

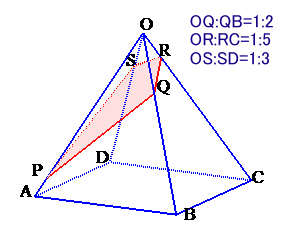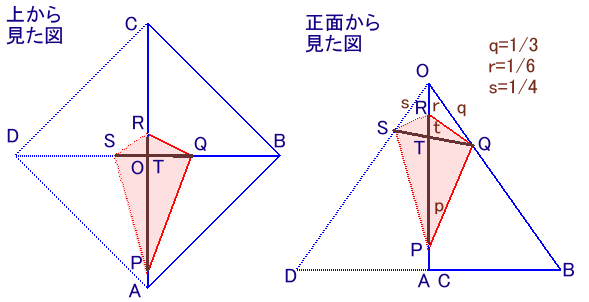
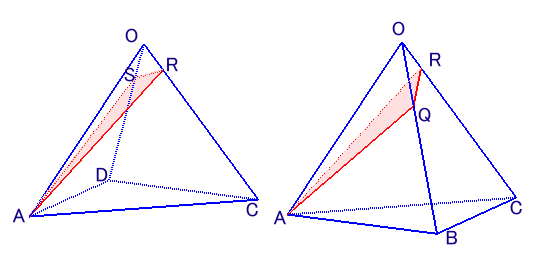
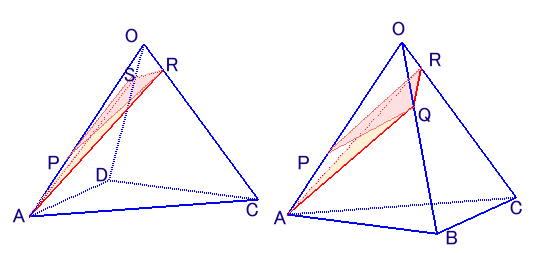
左図は、底面が正方形で、ＯＡ＝ＯＢ＝ＯＣ＝ＯＤ、体積が１４４cm3である正四角錐Ｏ −ＡＢＣＤを表しています。

いま、３点Ｑ、Ｒ、Ｓを通る平面でこの正四角錐を切断します。点ＱはＯＢを１：２に分ける点、点ＲはＯＣを１：５に分ける点、点ＳはＯＤを１：３に分ける点です。すると、切断面は図の四角形ＰＱＲＳになりました。

このとき、立体Ｏ−ＰＱＲＳの体積は何cm3でしょうか。

解答例１

佐藤 広宣さん、sugitakukunさん、トトロ＠Ｎさん、Taroさん、拓パパさん、うのたかはるさん、カステラ一番TZさん、遠い山のぽきょぽんさん、長野　美光さん、小西孝一さん、M.Hossieさん、ミミズクはくず耳さん、武田浩紀さん、をめが(中3)さん、DrKさん、ねこやんさん、ふじさきたつみさん、solitonさん、ψ(プサイ)さん、Octo Fenixさん、kasamaさん、ROBさん、ちこりんさん、 他

SQとPRの交点をＴとし、p＝OP/OA、q＝OQ/OB、r＝OR/OC、s＝OS/ODとおきます。

参考図１

ＯＴは∠ＤＯＢを二等分するから、△ＯＤＢの面積を１とすると、
　△ＯＳＱ＝sq、△ＯＳＴ＝1/2×st、△ＯＴＱ＝1/2×qt

△ＯＳＱ＝△ＯＳＴ＋△ＯＴＱなので、sq＝1/2×(st＋qt)
従って、2/t＝1/s＋1/qが成り立ちます。

同様に、2/t＝1/p＋1/rが成り立つので、
 1/p＋1/r＝1/s＋1/q
 1/p＋６＝４＋３

よって、p＝１となり、点Pは頂点Aと一致することが分かります。

さて、正四角錐を平面OACで２分割します。

参考図２

三角錐A−CODと三角錐A-ROSの高さは共通だから、体積比は底面の面積比に等しい。

よって、
　三角錐A-ROS＝三角錐A−COD×1/４×1/６
　　　　　　　　　＝７２×1/４×1/６
　　　　　　　　　＝３cm3

 同様に、
　三角錐A-QOR＝三角錐A−BOC×1/６×1/３
　　　　　　　　　＝７２×1/６×1/３
　　　　　　　　　＝４cm3

よって、
　Ｏ−ＰＱＲＳ＝A-ROS＋A-QOR
　　　　　　　＝４＋３
　　　　　　　＝７cm3
と求まります。

答：　７cm3

以上

解答例２

CRYING DOLPHINさん、中村明海さん、 他

p=1を求めなくとも、解答例１で正四角錐を平面OACで２分割したときを拡張して考えます。

参考図３

三角錐P−ROSと三角錐A-ROSの高さの比はPO：AO＝pに等しい、
よって、
　三角錐P−ROS＝三角錐A−COD×1/４×1/６×p＝３p
　三角錐P−QOR＝三角錐A−BOC×1/６×1/３×p＝４p

同様に、正四角錐を平面OBDで２分割すると、
　三角錐P−QOS＝三角錐A−BOD×1/４×1/３×p＝６p
　三角錐R−QOS＝三角錐C−BOD×1/４×1/３×１/６＝１

従って、
　Ｏ−ＰＱＲＳ＝３p＋４p＝６p＋１
となります。

これから、p＝1、およびＯ−ＰＱＲＳ＝７cm3　が得られます。

（その他の解法）