第361問の解答
問題[ 平面図形]
|
|
|
|
|
|
|
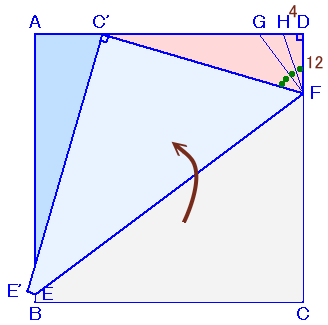 |
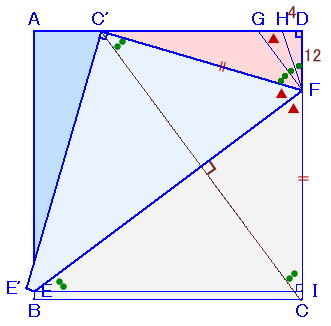
左図のような正方形ABCDがあります。 いま、頂点Cが辺AD上の点C'に重なるように折り返したところ、折り目が図のEFのようになりました。 また、△C'DFに注目して、∠C'FH:∠HFD=3:1になるように線分FHを引いたところ、HD=4cm、DF=12cmとなりました。 このとき、折り目EFの長さを求めてください。 |
|
|
|
|
|
|
解答例1
数楽者さん、Taroさん、佐藤 広宣さん、モルモット伯爵さん、DrKさん、有無相生さん、M.Hossieさん、kasamaさん、トトロ@Nさん、小西孝一さん、ミミズクはくず耳さん、 他多数
θ=∠HFD、EからBCと平行に引いた直線とCDの交点をIとします。
△FCC'はFC'=FCの二等辺三角形だから、
∠FC'C=∠FCC。ところが、∠FC'C+∠FCC=4θより、
∠FC'C=∠FCC=2θ=∠GFD。∠FEI=∠FC'C=2θだから、△FEIと△FGDは相似と分かります。
さて、三角関数の倍角公式により、
tanθ=HD/DF=1/3。従って、
tan2θ=2tanθ/(1−tan2θ)
=2×1/3/(1−(1/3)2)
=3/4。tan4θ=2tan2θ/(1−tan22θ)
=2×3/4/(1−(3/4)2)
=24/7。よって、
△FGD、△FEIは、三辺の比が3:4:5、
△FC'Dは、三辺の比が7:24:25
の直角三角形と分かります。従って、
C'F=DF×25/7=300/7cm、
DC=DF+FI
=DF+C'F
=12+300/7
=384/7cm。よって、
EF=EI×5/4
=DC×5/4
=384/7
=480/7cm
と求まります。なお、△FEIと△C'CDが合同より、EF=CC'が成り立ちます。
答: 480/7cm
以上
解答例2
拓パパさん、マサルさん、佐藤 広宣さん、すてっぷさん、dottoreさん、ふじさきたつみさん、遠い山のぽきょぽんさん、Octo Fenixさん、 他
解答例1とほぼ同じですが、三角関数を使用しないで計算しましょう。
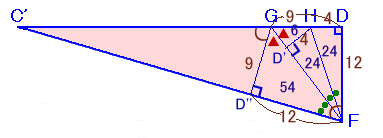
HからGFに下ろした垂線の足をD'、GからC'Fに下ろした垂線の足をD''とします。
△FDHと△FD'Hは合同で、
△FDH=△FD'H=1/2×12×4=24cm2。△HGD'と△FGDについて、∠Gは共通、∠HD'G=∠FDG=90度より
2つの三角形は相似で、相似比はHD':FD=4:12=1:3。よって、△HGD':△FGD=1:9、
△FGD:四角形HD'FD=9:8、
従って、△FGD=四角形HD'FD×9/8=24×2×9/8=54cm2。よって、GD=54/12×2=9cmとなります。
ここで、GD:FD=9:12=3:4なので、
△FDGは辺の比が3:4:5の直角三角形となります。また、△FDGと△FD''Gは合同で、
△FD''G=△FDG=54cm2。△GC'D''と△FC'Dは、∠C'は共通、∠GD''C'=∠FDC'=90度より
2つの三角形は相似で、相似比はGD'':FD=9:12=3:4。よって、△GC'D'':△FC'D=9:16、
△GC'D'':四角形GD''FD=16:7、
従って、△FC'D=四角形GD''FD×16/7=54×2×16/7=1728/7cm2。よって、C'D=(1728/2)/12×2=288/7cmとなります。
ここで、FD:C'D=12:288/7=7:24なので、
△FDGは辺の比が7:24:25の直角三角形となります。さて、△CDC'は△FDGと相似な直角三角形なので、辺の比は3:4:5。
よって、CC'=C'D×5/3=288/7×5/3=480/7cm。従って、EF=CC'=480/7cmと求まります。
(その他の解法)
- 三平方の定理、余弦定理を使って計算 ・・・ takaisaさん、 他