第362問の解答
問題[平面図形]
|
|
|
|
|
|
|
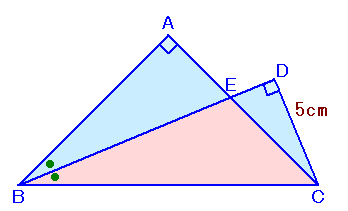 |
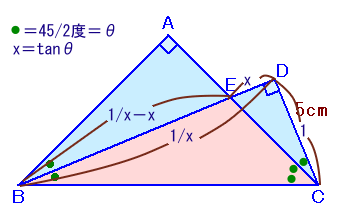
上の図のような∠A=90°の直角二等辺三角形ABCがあります。 いま、∠Bの二等分線に、点Cから下ろした垂線の足をDとします。また、BDとACの交点をEとします。すると、CD=5cmになりました。 このとき、△BECの面積を求めてください。 |
|
|
|
|
|
|
解答例1
高田修成さん、Taroさん、DrKさん、kasamaさん、ハラギャーテイさん、Toru Fukatsuさん、中村明海さん、M.Hossieさん、天秤さん、大岡 敏幸さん、 他多数
三角関数を使って考えてみましょう。
θ=45/2=22.5度、x=tanθとおきます。
CDの長さを1とすると、
ED=CDtanθ=x、BD=CD/tanθ=1/x
より、
BD=1/x−x=(1−x2)/x
と表せます。倍角公式より、
tan2θ=2tanθ/(1-tan2θ)=tan45°=1
よって、
1=2x/(1-x2)
従って、
(1−x2)/x=2よって、BD=2×5=10cmと分かります。
従って、
△BEC=1/2×BE×CD
=1/2×10×5
=25cm2
と求まります。(BEを求める別法)
1/tanθ-tanθ=cosθ/sinθ-sinθ/cosθ
=(cos2θ-sin2θ)/cosθsinθ
=2cos2θ/sin2θ
=2tan2θ
=2
BE=(1/tanθ-tanθ)・CD=2・5=10BE・cosθ=AB、BC・sinθ=CD=5
BE・BC・cosθsinθ=AB・5
BE・BC・cos2θ=AB・5・2
BE・AB=10・AB
BE=10答: 25cm2
以上
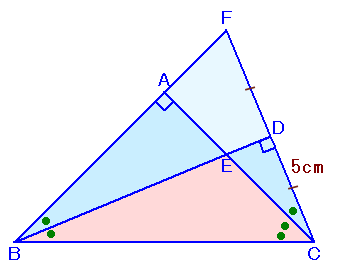
解答例2
CRYING DOLPHINさん、オモシロ※※館館長「影」さん、 他
|
|
|
|
|
|
|
|
|
|
|
|
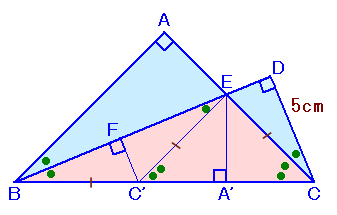
解答例3
菱沼聖子さん、 他
|
|
|
|
|
|
|
|
|
|
|
|
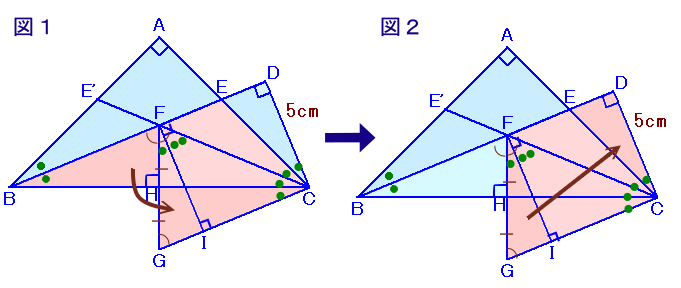
解答例4
小西孝一さん、遠い山のぽきょぽんさん、すてっぷさん、 他
|
|
|
|
|
|
|
|
|
|
|
|
解答例5
ふじさきたつみさん、 他
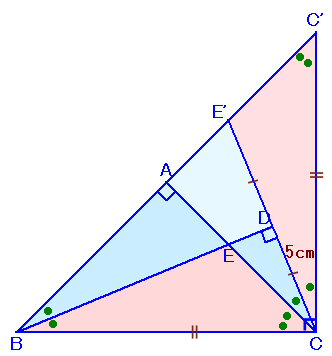
CからBCに垂直線を引きCC'=BCとなるようにC'をとり、
CDの延長線とBC'の交点をE'とします。
すると、△C'BCは二等辺直角三角形となるので、∠BC'C=45度となります。
よって、△E'CC'と△EBCは合同となりますので、E'C=EBとなります。
また、△BE'Dと△BCDは合同となるので、E'D=CD=5cm。
よって、EB=E'C=10cmと求まります。
以下、同様。