第364問の解答
問題[割合?]
|
|
|
|
|
|
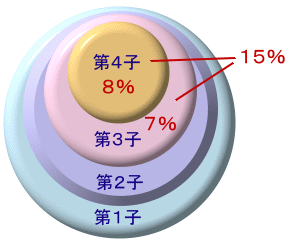
マサル王国は、「子供は4人まで」と法律で決められた国です。また、全国民がちょうど100歳まで生きる奇跡の国です。 この国の毎年の出生調査では、その年に生まれた子供全体の45%が(夫婦にとって)1人目の子供で、32%が2人目の子供、15%が3人目の子供、8%が4人目の子供となっており、これは過去数百年、ず〜っと続いているそうです。 では、この国の33歳の国民全員に「あなたの兄弟は自分も含めて何人ですか?」という質問をしたとき、「3人兄弟です」と答える人は全体の何%でしょうか。 |
|
|
|
|
|
解答例1
Taroさん、takaisaさん、拓パパさん、小西孝一さん、M.Hossieさん、 ろろさん、他多数
どの年齢でも、
第1子:第2子:第3子:第4子=45%:32%:15%:8%
だから、国民全体でも同じ割合と考えられます。従って、3人兄弟の末っ子は、第3子−第4子=7%の割合であり、
それぞれに兄が2人ずついるはず(故人となった兄は考慮しない)ですので、
兄弟全員では7%×3=21%と考えられます。答: 21%
以上
解答例2
あだださん、トトロ@Nさん、Miki Sugimotoさん、kasamaさん、ψ(プサイ)さん、 すてっぷさん、ラゴさん、大岡 敏幸さん、tomhさん、 他多数
次のような仮定を設けます。
毎年の出生数は一定 で、男女同じ割合で生まれる
極端に年齢の離れた兄弟はない(第1子と第4子の差も最大32)
双子以上はなし
結婚、第1子、第2子、・・が生まれる年齢および割合は皆同じ
そこで、各年ごとの人口をNとし、このうちM組の夫婦ができるものとします。
各夫婦のうち、最終的な子供の人数によって区分し、それらの割合を、
P0、P1、P2、P3、P4とします。すると、毎年生まれるの子供の数は、
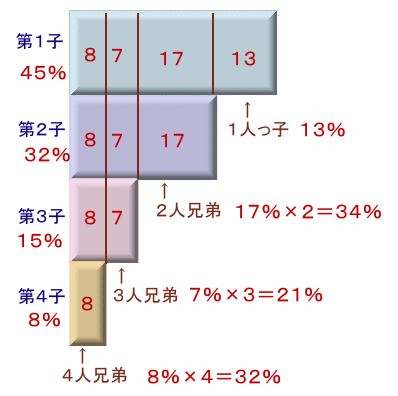
第1子:M×(P1+P2+P3+P4)=N×45% ・・・ (1)
第2子:M×( P2+P3+P4)=N×32% ・・・ (2)
第3子:M×( P3+P4)=N×15% ・・・ (3)
第4子:M× P4 =N×8% ・・・ (4)
(1)−(2)より、M×P1=N×13%
(2)−(3)より、M×P2=N×17%
(3)−(4)より、M×P3=N×7%
(4)より、M×P4=N×8%これらのうち、最終的に3人兄弟となるのは、
第1子:M×P3、第2子:M×P3、第3子:M×P3、第4子:なし
となるので、
合計=M×P3×3
=N×7%×3
=N×21% 人
となります。従って、3人兄弟の割合は、
N×21%÷N=21%
と考えられます。