第３６５問の解答

問題［平面図形 （軌跡）］

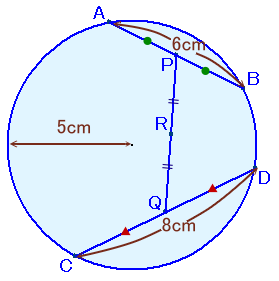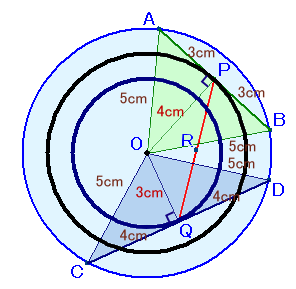
問題図 左図のような、半径が５cmの円があり、弦ＡＢ＝６cm、弦ＣＤ＝８cmとなっています。

いま、弦ＡＢの中点をＰ、弦ＣＤの中点をＱ、ＰＱの中点をＲとします。

弦ＡＢ、弦ＣＤがその長さを保ったまま自由に円上を動くとき、点Ｒが動くことのできる範囲の面積を求めてください。

解答例１

遠い山のぽきょぽんさん、長野　美光さん、うのたかはるさん、Taroさん、DrKさん、トトロ＠Ｎさん、kasamaさん、圭太さん、M.Hossieさん、ねこやんさん、高橋　道広さん、ラゴさん、ψ（プサイ）さん、sciberさん、他多数

まず点PおよびQの軌跡（動く範囲）を考えてみましょう。

参考図１

点Pは、OA＝OBの二等辺三角形△AOBの底辺ABの中点だから、
頂点Oから底辺ABに下ろした垂線の足になっています。
従って、△AOPと△BOPは合同な直角三角形になります。

また、OA＝５cm、AP＝６cm÷２＝３cmより、OP＝4cmと分かります。
よって、OPが常に４cmになることから、
点Pは点Oを中心とする半径４cmの円周上を動くことが分かります。

全く同様に、OQが常に３cmになることから、
点Qは点Oを中心とする半径３cmの円周上を動くことが分かります。


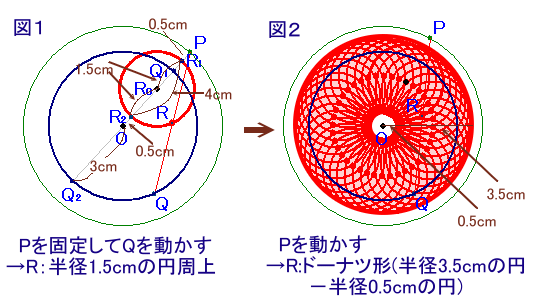
次に、点Pを固定して点Qを動かしたときの点Rの軌跡を考えてみましょう。（下記図１）

参考図２

点RはPQの中点なので、点Ｐが固定されているときには、
点Ｒは点Qが動く図形（円周）のちょうど２分の１の図形（円周）の上を動きます。

この円の中心はＰとＯの中点（Ｒ0とします）で、
Ｐと最も近い点Ｒ1はＰ、Ｑ、Ｏが一直線に並ぶときのＱ（Ｑ1とします）とＰの中点、
Ｐと最も遠い点Ｒ2はＰ、Ｏ、Ｑが一直線に並ぶときのＱ（Ｑ2とします）とＰの中点、
となります。

従って、ＯＲ1＝ＯＲ2＝０．５cm、円半径＝Ｒ0Ｒ1＝Ｒ0Ｒ2＝２cmとなります。

今度は、点Pを動かしたときに、この円が動く軌跡は、上記図２より、
点Oを中心とする半径３．５cmの円から点Oを中心とする半径０．５cmの円を
除いたドーナツ形の図形となります。

これが、求める点Rの軌跡全体になるので、
求める面積＝１/２×３．１４×３．５2−１/２×３．１４×０．５2
　　　　　　　＝１/２×３．１４×｛（７/２）2−（１/２）2｝
　　　　　　　＝１/２×３．１４×４８/２
　　　　　　　＝１２×３．１４
　　　　　　　＝３７．６８cm2
と求まります。

答：　３７．６８cm2

以上

（参考）点をドラッグして軌跡を確認する

　

（準備）

  1. 座標軸表示ボタンを押す

  2. 軌跡描画on/offボタンを押す

（軌跡描画）

  1. 点Qをドラッグして、点Rの軌跡を確認

  2. 点Pをドラッグして、点Rの軌跡を確認


操作法

このJavaAppletは愛知教育大の飯島先生他が作成したGC/Javaを利用しています。

　

解答例２

kuri, 他

参考図３

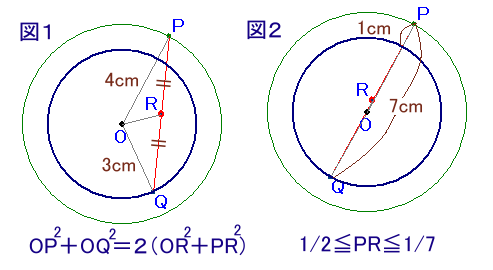
図１より、△OQPで点RはPQの中点だから、
　OP2＋OQ2＝２（OR2＋PR2）
　４2＋３2＝２（OR2＋PR2）
よって、
　OR2＝２５/２−PR2　・・・（１）

図２より、
　１≦PQ≦７
よって、
　１/２≦PR≦７/２

従って、（１）より、
　５０/４−（７/２）2≦OR2≦５０/４−（１/２）2
　１/４≦OR2≦４９/４
　１/２≦OR≦７/２　　・・・（２）

逆に（２）を満たす点Rに対して、点Rを通る適当な直線と２つの円の交点をP、Q
とし、（１）が成り立つように点Pを選べば、点RはPQの中点になります。

以上から、ORは点Oを中心とする半径7/2cmの円から半径1/2cmの円を除いた
ドーナツ形の図形内を動くことが分かります。

以下、同様。