第366問の解答
問題[確からしさ]
|
|
|
|
|
|
マサルさんとトモエさんが、1枚の10円玉を使って次のようなゲームをしています。 ルール:
2人はそれぞれ、3連続分の表、裏を予想する。 どちらかが代表で10円玉を投げ、2人の予想した3連続の出目が出るまで投げ続ける。 どちらかの予想した出目が出たところで終了し、予想が当たったほうを勝ちとする。 例えば、マサルさんが「裏→裏→表」、トモエさんが「表→裏→表」と予想していたとすると、
では、マサルさんが「表→裏→裏」を予想し、トモエさんが「表→表→裏」を予想するとき、 |
|
|
|
|
|
解答例1
DrKさん、拓パパさん、遠い山のぽきょぽんさん、ひだ弟さん、消しゴムパトロールさん、あ〜く@旧Nさん、高橋 道広さん、 他多数
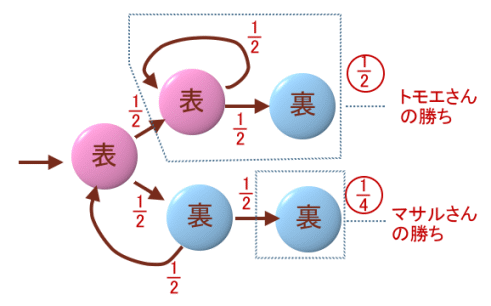
下図のような遷移図で考えてみましょう。
最初に表が出たところから本当の勝負が始まると考えていいでしょう。
ここから場合分けをします。
次に表が出たとき:
それ以降は結局トモエさんの勝ち ・・・ 1/2
次に裏が出たとき:
・さらに連続で裏が出るとマサルさんの勝ち ・・・ 1/4
・もし表が出たら最初からやり直し表→裏の繰り返しがあっても、各段階で
トモエさんが勝つ確率:マサルさんが勝つ確率=1/2:1/4=1:2
となっているので、
マサルさんが勝つ確率=1/3
と求まります。答: 1/3
以上
解答例2
小西孝一さん、武田浩紀さん、有無相生さん、 他
解答例1とほぼ同じですが、級数的に考えてみます。
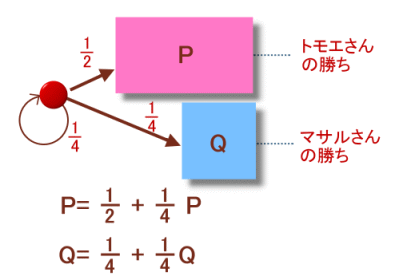
トモエさん、マサルさんの勝つ確率をP、Qとすれば、
トモエさんの勝ちは、最初に決まる場合(確率1/2)と2度目以降に決まる場合(1/4×P)の和
で表されるので、
P=1/2+1/4×P ・・・ (1)
同様に、マサルさんの勝ちは、
Q=1/4+1/4×Q ・・・ (2)
が成り立ちます。(1)、(2)より、
P=(1/2)/(1−1/4)=2/3
Q=(1/4)/(1−1/4)=1/3
と求まります。
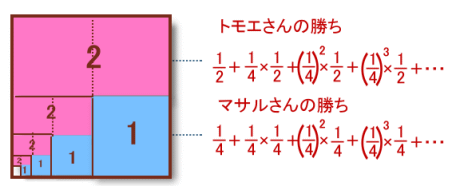
また、トモエさんの勝ちが、
最初:1/2
2回目:1/4×1/2
3回目:(1/4)2×1/2
4回目:(1/4)3×1/2
・・・・
なので、
P=1/2+1/4×1/2+(1/4)2×1/2+(1/4)3×1/2+・・・ (3)
同様に、マサルさんの勝ちは、
Q=1/4+1/4×1/4+(1/4)2×1/4+(1/4)3×1/4+・・・ (4)
と表されます。(3)×1/4、(4)×1/4より、
P×1/4= 1/4×1/2+(1/4)2×1/2+(1/4)3×1/2+・・・ (3)'
Q×1/4= 1/4×1/4+(1/4)2×1/4+(1/4)3×1/4+・・・ (4)'(3)−(3)'および(4)−(4)'より、
P−P×1/4=1/2、よってP=2/3
Q−Q×1/4=1/4、よってQ=1/3
と求まります。