第３６７問の解答

問題［平面図形］

問題図

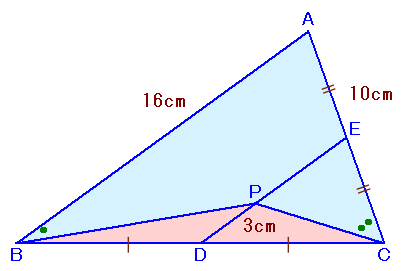左図のようなＡＢ＝１６cm、ＡＣ＝１０cmの△ＡＢＣがあります。

いま、辺ＢＣの中点をＤとし、Ｄを通りＡＢに平行な直線が辺ＡＣと交わる点をＥとします。さらにＤＥ上にＤＰ＝３cmとなる点Ｐをとり、頂点Ｂ、頂点Ｃと結んだところ、∠ＡＣＰの大きさは∠ＡＢＰの大きさの２倍となりました。

このとき、△ＢＰＣの面積を求めてください。

解答例１

長野　美光さん、あ〜く＠旧Ｎさん、きょろ文さん、DrKさん、モルモット大臣さん、柿原さん、有無相生さん、ちこりんさん、evolutionさん、M.Hossieさん、 他多数

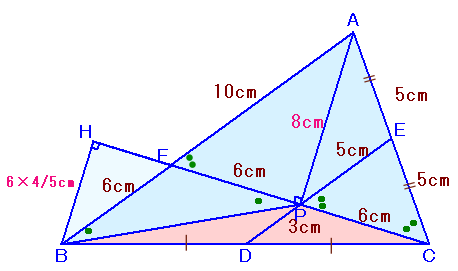
CPの延長線とABの交点をFとし、Bから直線CFに下ろした垂線の足をHとします。

参考図１

△CBFについて、DはCBの中点で、DPとBFが平行だから、
中点連結定理より、DP＝BP×１/２、
よって、BF＝DP×２＝３×２＝６cmとなります。

従って、AF＝AB−BF＝１６−６＝１０cm、
よって、△AFCは、AF＝ACの二等辺三角形となります。

従って、∠AFP＝∠ACP＝∠FBP×２となり、
また、∠AFPは△FBPの外角より、
　∠FPB＝∠AFP−∠FBP＝∠FBP。

よって、△FBPは、FB＝FP＝６cmの二等辺三角形となります。

また、△CAFについて中点連結定理より、PC＝FP＝６cm、
△AFCは二等辺三角形だから、APはFCの垂直二等分線、
よって、△AFPと△ACPは合同な直角三角形となります。

ところが、AF＝AC＝１０cm、FP＝CP＝６cmより、
これらは三辺の比が３：４：５の直角三角形となり、
よって、AP＝８cmと分かります。　・・・・　（１）

さて、△BFHは△AFPと相似な直角三角形となるので、
BH＝ＢＦ×ＡＰ/ＡＦ＝６×８/１０＝４．８cmとなります。

よって、
　△BPC＝１/２×PC×BH＝１/２×６×４．８＝１４．４cm2
と求まります。

答：　１４．４cm2

以上

解答例２

拓パパさん、DrKさん、高橋　道広さん、小西孝一さん、あほあほまんさん、 他

参考図２

（１）までは、解答例１と同じ。

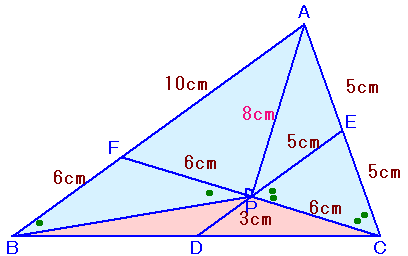
△AFC＝１/２×FC×AP
　　　　＝１/２×１２×８
　　　　＝４８cm2

△CAFと△CFBは底辺をAF、FBとみると、高さが共通なので、
△CAF：△CFB＝AF：FB＝１０：６。

よって、
　△CFB＝△CAF×６/１０＝４８×６/１０＝２８．８cm2。

△BFPと△BPCは底辺をFP、PCとみると高さが共通なので、
△BFP：△BPC＝FP：PC＝６：６。

従って、△BFP＝△BPC＝△BFC×１/２＝２８．８×１/２＝１４．４cm2
と求まります。

（その他の解法）