第368問の解答
問題[場合の数]
|
|
|
|
|
|
|
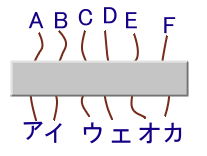 |
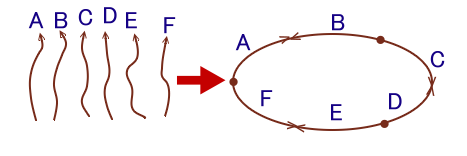
左図のように、板の下に6本の糸が隠れています。両端はそれぞれ一方が板の上のほう(A〜F)に、もう一方が 下のほう(ア〜カ)に出ています。 いま、A〜Fおよびア〜カをそれぞれ2つずつ3組にして結ぶとき、板を外すと糸が1つの大きな輪になっているような結び方は何通りあるでしょうか。 |
|
|
|
|
|
|
解答例1
拓パパさん、小西孝一さん、中村明海さん、あ〜く@旧Nさん、tekiさん、M.Hossieさん、すてっぷさん、ちこりんさん、きょろ文さん、ψ(プサイ)さん、航介さん、mhayashiさん、 他多数
|
|
|
|
|
|
|
|
|
|
|
|
解答例2
sugitakukunさん、中村明海さん、オモシロ※※館館長「影」さん、長野美光さん、 他
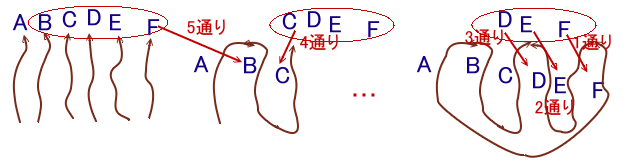
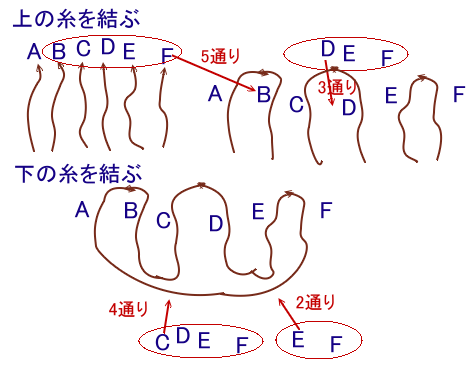
まず、上側を2本ずつの3組に分けてみます。
Aと同じ組にする1本を残り5本から選び(仮にBとします)ます。
次に残った4本のうち1本(仮にCとします)と同じ組にする1本を残り3本から選びます。
(仮にDとします)最後に残った2本(E、F)は自動的に同じ組になりますから、
3組に分けるのは、5×3=15通り
となります。さて、選んだ2本ずつの上側を結んでおきます。
次に、最初の組のBと結ぶ糸をC、D、E、Fの中から1本選びます。
(仮にCとします)BとCが同じく組になり、それぞれの下側を結ぶことになります。さらに、Cと同じ組のDと結ぶ糸(Dと同じ組にする)を、残ったE、Fの中から1本選びます。
(仮にEとします)DとEが同じ組になり、それぞれの下側を結びます。最後に、残ったEとAが自動的に同じ組になりますので、下側を結べば大きな輪になります。
従って、下側の組み合わせは、4×2=8通りとなるので、
合わせて求める結び方は=15×8=120通りになります。