第369問の解答
問題[平面図形]
|
|
|
|
|
|
|
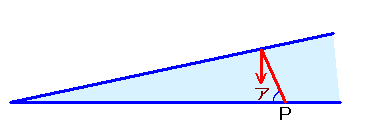 |
左図は、合わせ鏡上の点Pから光を発射したところを表しています。(上から見た図) まず、図中のアの角度が76°になるようにして光を発射したところ、光は3回反射して、Pに戻ってきたそうです。 では、光が7回反射してPに戻ってくるようにするには、アの角度を何度にすれば良いでしょうか。 |
|
|
|
|
|
|
解答例1
長野 美光さん、Taroさん、evolutionさん、M.Hossieさん、小西孝一さん、大岡 敏幸さん、 他
反射の問題は、折り返しで考えるといいでしょう。
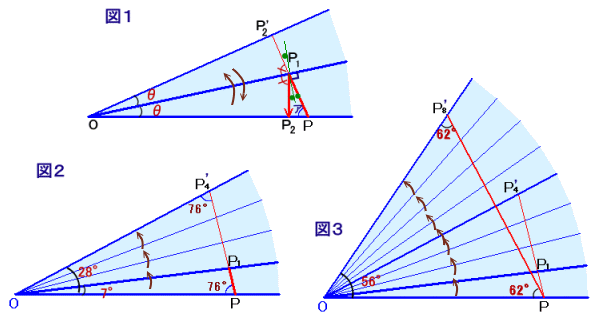
図1で、合わせ鏡の角度をθとし、対向する鏡の面でこちら側の面を折り返します。
Pから発射した光線がP1で反射し、元の面のP2に戻ってくるものとします。PP1の延長して折り返された面との交点をP'2とし、∠PP1P2の二等分線引くと、
∠OP1P2=∠OP1P'2=90°−∠PP1P2×1/2。よって、△P1OP2と△P1OP'2は、一辺と両端の角が等しいので合同。
従って、OP'2=OP2となり、P2を求めるにはP'2は逆に折り返すといいことが分かります。さて、光線が3回反射して元のPに戻ったということは、
合わせ鏡を3回折り返した面とPP1の延長との交点をP'4とすると、
OP4=OP'4となることを意味します。 ・・・ 図2よって、△OP4P'4は二等辺三角形となりますので、
頂角P4P'4O=180−76×2=28度、
従って、合わせ鏡の角度=28÷4=7度となります。さて、光線が7回反射して元のPに戻るためには、合わせ鏡を7回折り返した面で
OP'8=OP8となる点P'8へ向かって光線を発射すればいいことになります。 ・・・ 図3よって、△OP8P'8は二等辺三角形となりますので、
∠OP8P'8=(180−7×8)÷2=62度
と求まります。答: 62度
以上
解答例2
DrKさん、kasamaさん、有無相生さん、小学名探偵さん、CRYING DOLPHINさん、 他
各反射では、入射角=反射角が成り立っています。
合わせ鏡の角度をθ、最初の点PをP0、各反射点をP1、P2、・・・、
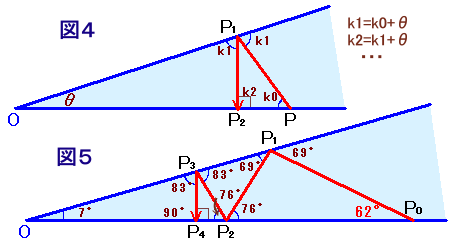
および各入射角をk0、k1、k2とします。△P0P1P2について、k1は外角なので、k1=k0+θ が成り立ちます。
同様に、k2=k1+θ、k3=k2+θ、・・・・ となります。 ・・・ 図4さて、最初に光線を76°で発射したとき、3回の反射で元の点に戻ったことから、
2回目の反射では入射角がちょうど直角になり、以降元に戻ったものと考えられます。従って、k2=k0+2θ=76+2θ=90°
よって、θ=(90−76)÷2=7°となります。
このとき、各入射角は、76、83、90、83、76となっています。次に、7回の反射で元の点に戻るということは、4回目の反射の入射角が直角。
よって、k4=k0+4θ=k0+4×7=90°、
よって、k0=90−28=62°と求まります。
このとき、各入射角は、62、69、76、83、90、83、76、69、62となっています。
(その他の解法)
- 作図して各角度を求める ・・・ ポケモンハルカさん、ψ(プサイ)さん、 他