第３７０問の解答

問題［空間図形］

問題図

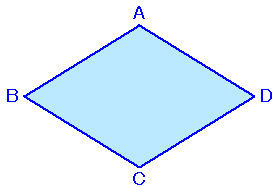左図のような、厚紙を切って作った合同な菱形がたくさんあります。この菱形を何枚か使うと、次のような条件を満たす立体を作ることができます。

  1. 菱形の鋭角（図のＢ、Ｄ）の頂点が５つ集まって、１つの頂点が出来る。
  2. 菱形の鈍角（図のＡ、Ｃ）の頂点が３つ集まって、１つの頂点が出来る。
  3. 凹んでいない立体である。

このとき、完成した立体について、面の数、および頂点の数は、それぞれいくつでしょうか。

解答例１

中村明海さん、CRYING DOLPHINさん、トトロ＠Ｎさん、あ〜く＠旧Ｎさん、ｎａｍａさん、nさん、他

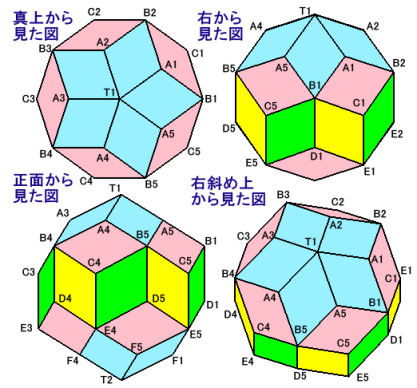
求める立体は、結論からいうと下記のような菱形３０面体になります。

参考図１

面の数は、上から
　青：５個、　赤：５個、　緑・黄：５個ずつ、　赤：５個、　青：５個
の合計２０個。

頂点の数は、上から、
　T１、A1〜A5、B1〜B5、C1〜C5、D1〜D5、E1〜E5、F1〜F5、T２
の合計３２個となります。

　

答：　面＝３０個、頂点＝３２個

以上

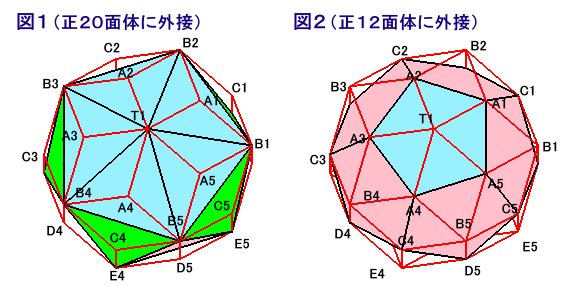
さて、この菱形３０面体は、正２０面体または正１２面体を元に、各面の中心を持ち上げることで得られます。

参考図２

実は、正２０面体と正１２面体の双対性から、どちらも同じ立体が得られるのですが、詳しいことは省略します。

（正２０面体に外接する場合）

  • 面の数　・・・　正２０面体の各辺と、菱形の長い対角線（Ｌとします）が１：１に対応するので、正２０面体の辺の数と同じ３０個

  • 頂点の数　・・・　正２０面体の頂点と共通のもの１２個と、各面の中心を持ち上げた２０個の合計３２個

（正１２面体に外接する場合）

  • 面の数　・・・　正１２面体の各辺と、菱形の短い対角線（Ｓとします）が１：１に対応するので、正１２面体の辺の数と同じ３０個

  • 頂点の数　・・・　正１２面体の頂点と共通のもの２０個と、各面の中心を持ち上げた１２個の合計３２個

ここまでで、菱形３０面体が条件を満たす立体の１つであることは示されます（十分条件）。
　

さて、求める立体は菱形３０面体しかないこと（必要条件）は、どう示せばよいでしょうか？
正２０面体の例で考えてみましょう。　・・・　図１

まず、求める立体で鋭角の頂点５個が集まったある頂点をとりＴ1とします。
また、Ｔ1を含む５個の菱形に関して鈍角のものをA1〜A5、鋭角のものをB1〜B5とします。
ここまでで５個の菱形が星形状に集まった図形が一意的にできます。

次に、A1〜A5には、それぞれ菱形が２個ずつ集まっているので、もう１個ずつは一意的に決まります。これらの対角線上の頂点をC1〜C5とします。

すると、△Ｔ1B1B2、△Ｔ1B2B3、△Ｔ1B3B4、△Ｔ1B4B5、△Ｔ1B5B1の各辺は、いずれも長さはＬに等しいので、正三角形であることが分かります。

正三角形５枚を１つの頂点に集めてできる図形は一意的に決まるので、求める立体のここまで決まった部分は、Ｌを１辺とする正２０面体の上に乗っていることが分かります。

以下、同様に求める立体の残りの菱形をつなぎ合わせていくと全ての頂点がきまり、ちょうどこの正２０面体の上に乗っていることが分かります。

正１２面体の場合も、同様に示されます。
　

（参考）菱形３０面体の菱形は対角線の比率が黄金比となること

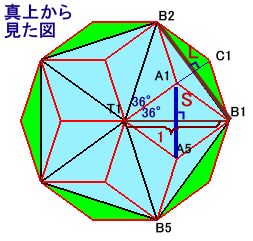
参考図２−２

上の図は、図１を真上から見た図で、各辺の長さは水平に見た長さで考えます。
いまT1B1の長さを１とおくと、T1B1とA1A5の中点は菱形の中心で一致します。

よって、
　A1A5＝T1B1×１/２×tan36°×２＝tan36°　・・・　（１）

また、B1B2とA1C1の中点は菱形の中心で一致し、C1はT1A1の延長上にあるので、
　B1B2＝T1B1×sin36°×２＝sin36°×２　・・・　（２）

さて、A1A5およびB1B2は、どちらも水平なのでそれぞれS、Lの長さと等しくなります。

よって、
　L/S＝（sin36°×２）/tan36°
　　　＝cos36°×２
　　　＝（１＋√５）/４×２
　　　＝（１＋√５）/２
を得ます。
まさに、これは黄金分割の比率に他なりません。

以上は、長野美光さんのホームページ（ヨッシーの算数・数学の部屋）を参考にさせて頂きました。

解答例２

長野　美光さん、小西孝一さん、M.Hossieさん、すてっぷさん、
 　takaisaさん、naopapaさん、ねこやんさん、kasamaさん、遠い山のぽきょぽんさん、DrKさん、他

面(Face)の数、点(Vertex)の数、辺(Edge)の数をそれぞれＦ、Ｖ、Ｅ とします 。
Ｆ、Ｅ、Ｖに関する方程式を考えて解いてみましょう。

参考図３

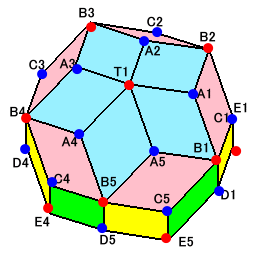
各面に対して内角が鋭角の頂点（●）が２個、鈍角の頂点（●）が２個ずつあります。
鋭角の頂点１個を５つの面が共有し、鈍角の頂点１個を３つの面が共有していることから、
　Ｖ＝Ｆ×２/５＋Ｆ×２/３＝Ｆ×１６/１５　・・・　（１）
が得られます。

また、各面に４辺がありますが、１つの辺を２つの面で共有していることから、
　Ｅ＝Ｆ×４×１/２＝Ｆ×２　・・・　（２）
が成り立ちます。

（１）、（２）から面の数Ｆは１５の倍数となりますが、これだけでは決まりません。
ここで、多面体に関するオイラーの定理から、
　Ｖ＋Ｆ−Ｅ＝２　・・・　（３）
が成り立ちます。

（１）、（２）の式を（３）に代入して、
　Ｆ×１６/１５＋Ｆ−Ｆ×２＝２
　Ｆ×１/１５＝２
よって、Ｆ＝２×１５＝３０が得られます。

これを（１）、（２）に代入して、
　Ｖ＝３０×１６/１５＝３２、
　Ｅ＝３０×２＝６０
が得られます。

なお、ここまでは条件を満たす立体が存在したらという必要条件のみの議論なので、条件を満たす立体が確かに存在する（十分条件）ということについて別途示す必要があります。

（その他の解法）