第372問の解答
問題[平面図形]
|
|
|
|
|
|
|
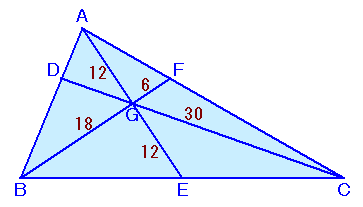 |
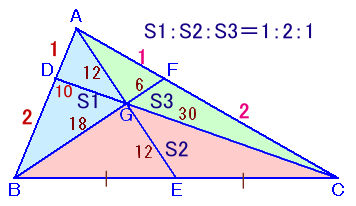
左図のような△ABCがあります。 辺BC上に点Eをとり、AG=GE=12cmとなる点をGとします。また、直線BGと辺ACの交点をFとすると、BG=18cm、GF=6cmとなりました。さらに、線分CGの長さは30cmとなりました。 このとき、△ABCの面積を求めてください。 |
|
|
|
|
|
|
解答例1
中村明海さん、たみてんさん、小西孝一さん、あ〜く@旧Nさん、kataさん、ミミズクはくず耳さん、すてっぷさん、M.Hossieさん、をめがさん、UnderBirdさん、他多数
まず、BE=ECとなることを示しましょう。
S1=△GBC、S2=△GBC、S3=△GBCとおき、面積比を求めます。
△ABG:△BGE=△AGC:△CGE:=AG:GE=1:1、
(△ABG+△AGC):(△BGE+△CGE)=(S1+S3):S2=1:1
よって、S2=S1+S3 ・・・ (1)同様に、(S1+S2):S3=BG:GF=3:1
よって、 S1+S2=3S3 ・・・ (2)(1)、(2)より、
S1+(S1+S3)=3S3
S3=S1
(1)より、
S2=2S1従って、
S1:S2:S3=1:2:1
となります。よって、
BE:EC=S1:S3=1:1、AD:DB=S3:S2=1: 2、AF:FC=S1:S2=1:2、
および、
CG:GD=(S2+S3):S1=3:1
が示されます。さて、ここから∠BGE=90°を示します。
算チャレ的図形の回転で解くと次のようになります。(中村明海さん他)
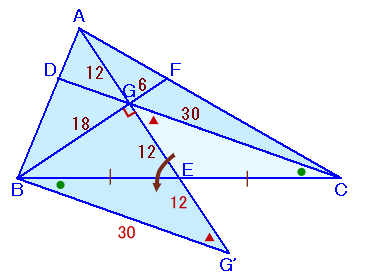
点Eを中心にして△GECを回転し、CをBに重ねた三角形をG'EBとします。
すると、∠GEB+∠BEG'=∠GEB+∠CEG=180°より、
点G、E、G'は一直線上に並びます。△GBG'において、
GB=18cm、GG'=GE×2=24cm、BG'=CG=30cm
となり、
GB:GG':BG'=18:24:30=3:4:5従って、△GBG'は、∠BGG'=90°の直角三角形になります。
△GBC=△GBG'=1/2×BG×GG'=1/2×18×24=216cm2
よって、
△ABC=△GBC×2=432cm2 と求まります。答: 432cm2
以上
(別解1)あ〜く@旧Nさん他
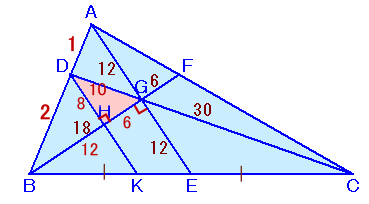
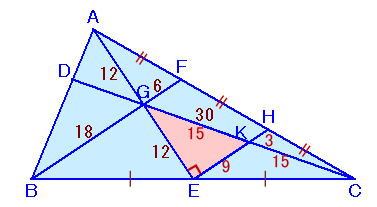
点Dを通り直線AEに引いた直線とBCの交点をKとし、DKとBFの交点をHとします。
AEとDKは平行だから、△ABGと△DBHは相似、
よって、GH:HB=AD:DB=1:2より、GH=6cm、HB=12cm。
また、AG:DH=AB:DB=3:2より、DH=8cmを得ます。従って、△DHGの三辺の比=6:8:10=3:4:5となり、直角三角形であることが分かります。
よって、DKおよびAEはBFと直交するので、
△ABE=1/2×AE×BG=1/2×24×18=216cm2
よって、
△ABC=△ABE×2=432cm2 と求まります。
(別解2)M.Hossieさん、 他
c=BE=ECとおきます。
中線定理により、 GB2+GC2=2(c2+GE2)、
182+302=2(c2+122)、
c2=(182+302)/2−122=468、
よって、c=√(468)=6√(13)となります。θ=∠BGCとおくと、△GBCに関して余弦定理より、
cosθ=(GB2+GC2−(2c)2)/(2GB×GC)
=−648/1080
=−3/5従って、
sinθ=√(1−cos2θ)=4/5
△GBC=1/2×GB×GC×sinθ
=1/2×18×30×4/5
=216cm2
よって、
△ABC=△GBC×2=432cm2 と求まります。
解答例2
takaisaさん、他
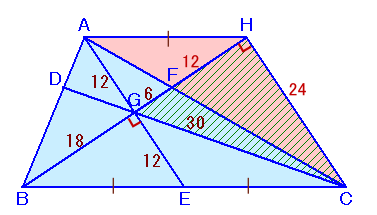
BGを延長し、GH=GB=18cmとなるように点Hを取ります。
△AGHと△EGBについて、AG=EG=12cm、GH=GB=18cm、∠AGH=∠EGBより、
二辺と挟角が等しいので合同。
従って、AH=BE、∠AHG=∠EBG、よってAHとBEは平行となります。すると、△AFHと△CFBは相似で相似比=FH:FB=12:24=1:2、
よって、AH:BC=1:2となり、BE=ECが成り立ちます。△GHCについて、GC:HC:GC=18:24:30=3:4:5となることから、
△GHCは、∠GHC=90°の直角三角形となることが分かります。よって、△GHC=1/2×GH×HC=1/2×18×24=216cm2。
AHとECが平行でAH=ECより、四角形AECHは平行四辺形、
よって、△AEC=△ACH=△GHC=216cm2。従って、△ABC=△AEC×2=432cm2 と求まります。
解答例3
yuhtoさん、高橋 道広さん、他
点Eを通りBFと平行に引いた直線とACの交点をHとし、EHとDCの交点をKとします。
GFとEHが平行だから、△AEHに関して中点連結定理より、
AF=FH、およびEH=GF×2=12cm。 ・・・ (1)今度は△CFBに関して、FBとHEが平行でFB:HE=24:12=2:1、
よって中点連結定理より、BE=EC、FH=HCがいえます。そして△CFGに関して再び中点連結定理より、
GK=KC=15cm、KH=GF×1/2=3cmとなり、
EK=EH−KH=12−3=9cmとなります。よって、△EKGに関して、EK:GE:GK=9:12:15=3:4:5より、
△EKGは∠GEK=90°の直角三角形となります。△AEH=1/2×AE×EH=1/2×24×12=144cm2。
△AEC=3/2×△AEH=216cm2(AH:AC=2:3だから)、
従って、△ABC=△AEC×2=432cm2 と求まります。
(その他の解法)
- ベクトルを用いて解く ・・・ Toru Fukatsuさん、 他
- 座標系で解く ・・・ 有無相生さん、 他