第３７３問の解答

問題［場合の数］

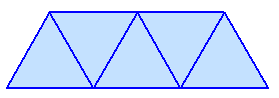問題図 左図のような図形を一筆書きする方法は何通りあるでしょうか。

ただし、始点と終点が逆になっただけのものは同じとします。

解答例１

たみてんさん、ヒデー王子さん、中村明海さん、すてっぷさん、 他

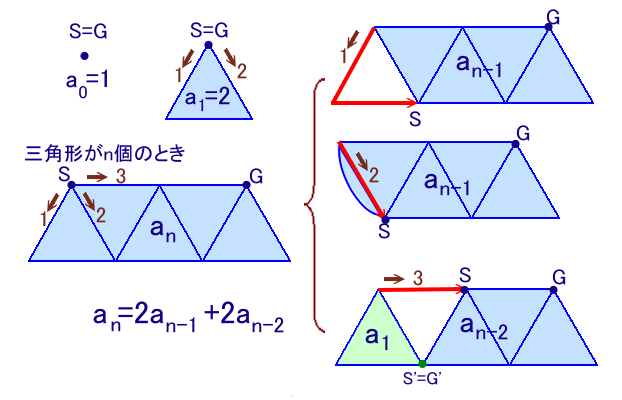
三角形がn個のときの一筆書きをan通りとし、nに関する漸化式を考えます。

参考図１

よく知られているように、一筆書きできる条件は、その図形に奇点（奇数個の線が集まる点と）の個数が０または２になることです。そして、

  • 奇点が０のとき　・・・　どの点から始めてもよく、最後に出発点に戻るようにすればよい

  • 奇点が２のとき　・・・　一方の奇点から始め、もう一方の奇点に戻るようにすればよい　

となっています。

  1. n=0のとき、何もない図形なので本来は意味がありませんが、頂点が１個の図形と考えれば、
    この点のみを書く１通りと考えられます。　・・・　a1＝１通り

  2. n=1のとき、始点が決まったものとすれば、右回りと左回りの２通りあります。　・・・　a1＝２通り

  3. n≧２のときには奇点がちょうど２個となります。
    一方の始点Ｓから出発するとき、方向は３通りあります。（上図参照）

  • 方向１：残りの図形は、三角形（n-1）個。　・・・　an-1通り

  • 方向２：残りの図形は、三角形（n-2）個と三角形1個が１点で結ばれたもの。
    　・・・　an-2×a1通り

従って、
　an＝２an-1＋２an-2
が成り立ちます。

n 0 1 2 3 4 5
an 1 2 6 16 44 120

よって、この漸化式にもとづいて順次計算していけば、a5＝１２０通りとなります。

　

答：　１２０通り

以上

解答例２

みかんさん、数楽者さん、Taroさん、CRYING DOLPHINさん、長野　美光さん、ちこりんさん、M.Hossieさん、大岡　敏幸さん、他多数

参考図２

解答例１で述べたとおり、奇 点から書き始める必要があります。

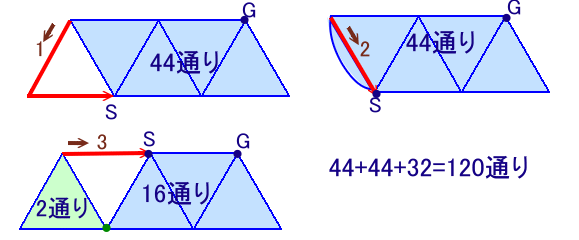
方向は３通りなので、それぞれの場合に分けて数え上げると、

  1. ４４通り
  2. ４４通り
  3. ３２通り

となり、
　合計＝４４＋４４＋３２＝１２０通りとなります。

（その他の解法）