第３７４問の解答

問題［場合の数］

１ｇ、４ｇ、１６ｇ、６４ｇ、２５６ｇの重りがそれぞれ２個ずつあります。
これらのおもりを使って、「天秤の片側にだけ重りを乗せる」方法で重さを測ることにします。

すると、例えば６ｇの重さは１ｇの重りを２個と４ｇの重りを１個使えば測ることができますが、７ｇの重さは測ることができません。

では、これらの重りを使って「天秤の片側にだけおもりを乗せる」方法で測れる重さのうち、２８９ｇは小さいほうから何番目の重さでしょうか？

解答例１

トトロ＠Ｎさん、たみてんさん、長野　美光さん、DrKさん、CRYING DOLPHINさん、あ〜く＠旧Ｎさん、敬＠Nさん、ちこりんさん、有無相生さん、小学名探偵さん、Taroさん、 他

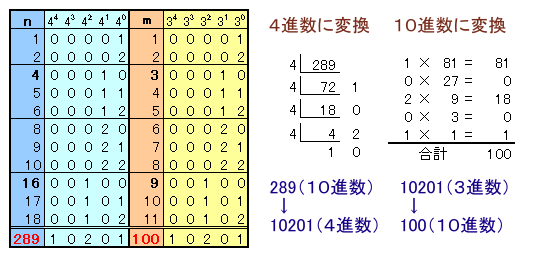
４進数および３進数の問題に帰着できます。

参考図１

各おもりは、１＝４0、４ｇ＝４1、１６＝４2、６４＝４3、２５６＝４4と４のべき乗になっています。

従って、ある重さ（nｇとします）の量り方は、nを４進数で表して、各桁の数字だけのおもりを使うと良いことになります。

たとえば、６ｇは６（１０進数）＝１２（４進数）なので、４ｇのおもり１個と１ｇのおもり２個で量れます。

同様に、２８９（１０進数）＝１０２０１（４進数）なので２５６ｇのおもり１個と１６ｇのおもり２個、および１ｇのおもり１個とで量ることができます。

さて、量れる重さ（mｇとします）とおもりの個数を順に見ていくと、おもりの個数はmを３進数で表したものに対応していることが分かります。

従って、１０２０１（３進数）を１０進数に変換すると１００になるので、２８９ｇは小さい方から１００番目ということになります。


なお、１０進数を４進数に変換するのは、４で割った商と余りを順番に計算したときに得られるあまりの数が各桁の数字となります。

また、３進数を１０進数に変換するには、３のべき乗の値に各桁の数字を掛けたものを合計することで得られます。

答：　１００番目

以上

（その他の解法）