第377問の解答
問題[速さの問題]
|
|
|
|
|
|
マサルさんと、弟のツヨシ君は、運動公園にやってきました。 マサルさんは日頃の運動不足を解消すべく、81m離れたA地点とB地点の間を毎分65mの速さで往復運動することにしました。ツヨシ君は、マサルさんの後を追いかけて毎分13mの速さで歩きますが、マサルさんとすれ違うとその場でまわれ右をして向きを変えてマサルさんの後を追いかけます。 2人が同時にA地点を出発したとすると、ツヨシ君が初めてAB間の真ん中の地点を通るのは、出発後いつの時点でしょうか。 |
|
|
|
|
|
解答例1
Taroさん、あ〜く@旧Nさん、DrKさん、すてっぷさん、みかんさん、あさみかずみさん、大岡 敏幸さん、ポケモンハルカさん、 さん、 他多数
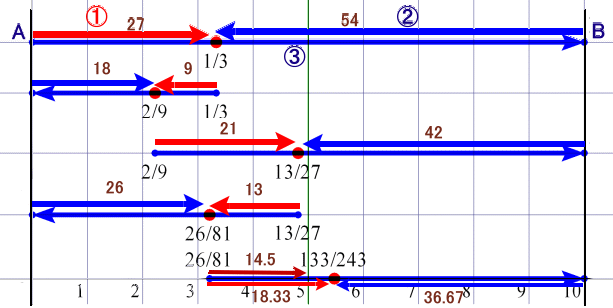
下図のような線分図で考えます。
(最初に出会う地点)
出発して二人が出会うまでに、マサルさんはBまで行って折り返すことになるので、
二人の移動距離合計はAB間の距離の2倍になります。二人の速度比=65:13=5:1なので、
ツヨシ君の移動距離を1とすると、マサルさんの移動距離は5。合計6がAB間の2倍だから、AB間の距離は3。
従って、出会う地点はABを1:2に内分する点で、
Aからの距離=81×1/3=27m
となります。(2度目に出会う地点)
同様に、次に出会う地点は、ここからAまでの距離27の1/3=9m、
Aからは27−9=18mの地点となります。(3度目に出会う地点)
次に出会う地点までの距離は、Bまでの距離63(=81−18)の1/3=21m、
Aからは18+21=39mの地点となります。(4度目に出会う地点)
次に出会う地点までの距離は、Aまでの距離39の1/3=13m、
Aからは39−13=26mの地点となります。(5度目に出会う地点)
次に出会う地点までの距離は、Bまでの距離55(=81−26)の1/3=18.33m、
Aからは26+18.33=44.33mの地点となりますので、
ここで初めてABの中間点を越えることになります。以上の間に、ツヨシ君が移動した距離合計は、
27+9+21+13+(81÷2−26)=84.5m
従って、所要時間は、
84.5m÷13m/分=6.5分
と求まります。答: 6分30秒後
以上
解答例2
たみてんさん、角さん、辻。さん、小西孝一さん、M.Hossieさん、中村明海さん、有無相生さん、他
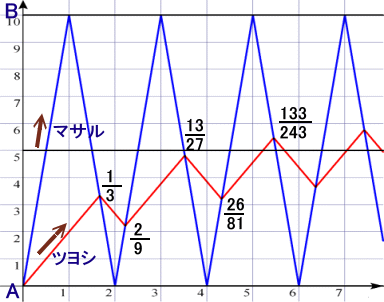
ダイヤグラムを参考に漸化式で考えます。
ツヨシ君はマサルさんを追いかけながらABの間を行ったり来たりします。
n回目にBに向かって進むときにマサルさんと出会う地点をQnとし、
今度Aに向かって戻るまでに出会う地点をPnとします。解答例1と同様にして、
AQn=APn-1+(1−APn-1)×1/3=1/3+2/3×APn-1 ・・・ (1)
APn=AQn×2/3=2/9+4/9×APn-1 ・・・ (2)(2)より、Pn、Qnの収束点(もしあれば)をP、Qとすれば、
AP=2/9+4/9×AP
より、
AP=2/9×9/5=2/5、AQ=1/3+2/3×AP=3/5
を得ます。(2)より、
APn−2/5=4/9×(APn-1−2/5)
APn−2/5=(4/9)n×(AP0−2/5)
よって、
APn=2/5−2/5×(4/9)n ・・・ (3)
(1)より、
AQn=1/3+2/3×APn-1
=1/3+2/3×{2/5−2/5×(4/9)n-1}
=3/5−3/5×(4/9)n ・・・ (4)よって、(3)、(4)より、Pn、Qnはnが大きくなるにつれ単調に増加しながら2/5および3/5に収束することが分かります。
(4)より、Qn≧1/2となるのは、n≧3のときとなります。
n回目の行き来でツヨシ君が移動する距離は、
(AQn−APn-1)+(AQn−APn)
={1/5+3/10×(4/9)n}+{1/5−1/5×(4/9)n}
=2/5+1/10×(4/9)nよって、n=1、2では、
2/5×2+1/10×{4/9+(4/9)2}
=70/813回目にABの中間点までツヨシ君が移動する距離は、
1/2−AP2
=29/162従って、ツヨシ君の移動距離合計は、
70/81+29/162=169/162実際の移動距離合計=169/162×81=169/2m
よって、所要時間=169/2÷13=13/2分
と求まります。
(その他の解法)
- プログラムで解く ・・・ ななおさん、他