第３７８問の解答

問題［平面図形］

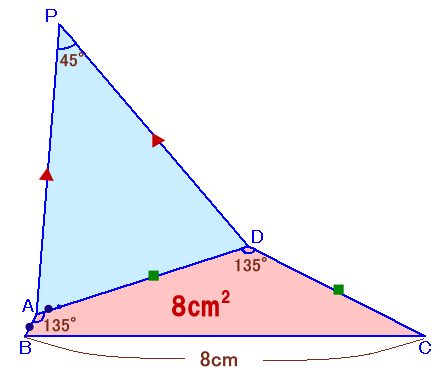問題図 左図で、四角形ＡＢＣＤは、ＢＣ＝８cm、∠ＢＡＤ＝∠ＡＤＣ＝１３５°、ＡＢ＋ＣＤ＝ＡＤで、面積が８cm2となっています。

また、△ＰＡＤは、ＰＡ＝ＰＤ，∠ＡＰＤ＝４５°の二等辺三角形です。

このとき、△ＰＡＤの面積を求めてください。

解答例１

はなうさん、まるケンさん、hiroさん、すてっぷさん、 他

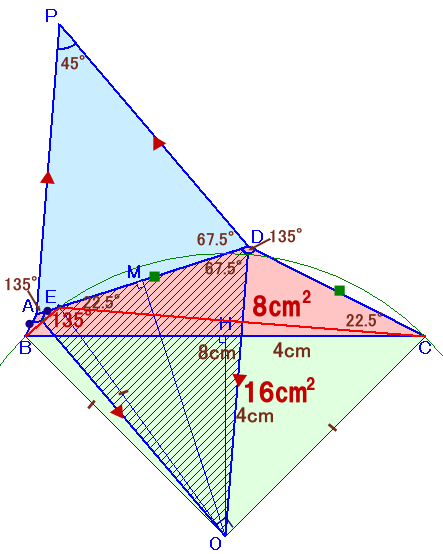
AD上に点Eを、AE＝ABとなるように取ります。

参考図１

AD＝AB＋CDより、
　DE＝AD−AE＝AD−AB＝CD。

従って、△ABE、△DECは、いずれも頂角が１３５度の二等辺三角形となり、
∠ABE＝∠AEB＝∠DEC＝∠DCE＝（１８０−１３５）÷２＝２２．５度となります。

よって、
　∠BEC＝１８０−（∠AEB＋∠DEC）＝１８０−４５＝１３５度となります。

ここで、△EBCの外接円の中心をOとすると、∠BEC＝１３５度＞９０度より、
中心Oは辺BCに関して点Eと反対側にあることになります。

∠BOC（外側）は弧BC（外側）の中心角であり、∠BECは円周角となっています。
従って、３６０−∠BOC（内側）＝∠BEC×２＝２７０度、
よって、∠BOC（内側）＝３６０−２７０＝９０度となります。

従って、△OBCは頂角が９０度の直角二等辺三角形となり、
底辺BC＝８cmなので、△OBC＝１/２×８×４＝１６cm2となります。

さて、△ABOと△AEOに関して、AB＝AE、BO＝EO、AOは共通より、
三辺が等しいので合同。

同様に、△DCOと△DEOも三辺が等しいので合同。

従って、∠OAD＝∠ODA＝１３５×１/２＝６７．５度。
また、∠PAD＝∠PDA＝９０−４５××１/２＝６７．５度。

よって、△PADと△OADは合同な二等辺三角形と分かります。

よって、
　△PAD＝△OAD
　　　　　＝△AEO＋△DEO
　　　　　＝（四角形ABCD＋△OBC）×１/２
　　　　　＝（８＋１６）×１/２
　　　　　＝１２cm2
と求まります。

（参考）多くの方は、ADを軸に△PADを折り返して解かれていました。
手順は異なりますが、内容的にはほぼ同じになります。
　

答：　１２cm2

以上

解答例２

CRYING DOLPHINさん、ねこやんさん、遠山のぽきょさん、他

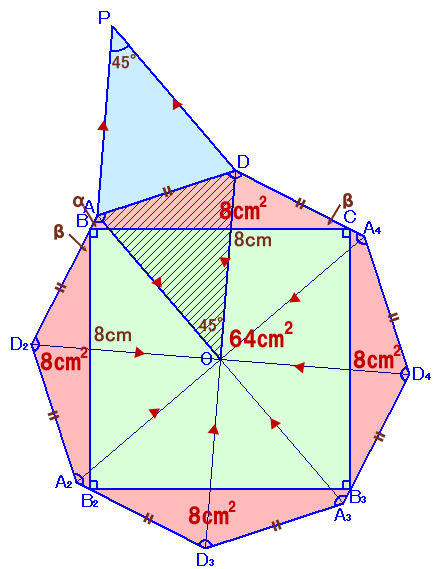
下図のように四角形ABCDを４個、底辺ACが正方形となるように並べます。

参考図２

四角形の内角の和は３６０度だから、
　∠ABC＋∠DCB＝３６０−（１３５＋１３５）＝９０度

よって、
　∠ABC＋∠CBB2＋∠D2BB2
＝∠ABC＋９０度＋∠DCB
＝１８０度

従って、点A、B、D2は一直線上に並びます。
また、AB＋BD2＝AB＋CD＝AD。

点A2、B2、D3と点A3、B3、D4および点A4、C、Dもについても同様。

よって、できた図形の外側の辺の個数は８つになり、辺の長さはすべてADに等しく、
しかも頂角はいずれも１３５度となるので、
これらは正八角形の周囲と一致することが分かります。

さて、
　正八角形の面積
＝四角形ABCD×４＋正方形BB2B3C
＝８×４＋８×８
＝９６cm2

一方、正八角形の中心をOとすると、
△OADは底辺がADで頂角（∠AOP）が４５度の二等辺三角形となるので、
△PADと合同。

よって、
　△PAD＝正八角形×１/８＝９６×１/８＝１２cm2
と求まります。

（その他の解法）